题目内容
7.已知直线l的参数方程为:$\left\{{\begin{array}{l}{x=1+\frac{1}{2}t}\\{y=\frac{{\sqrt{3}}}{2}t}\end{array}}\right.$(t为参数),曲线C1的极坐标方程为:ρ=1.(1)写出曲线C1的直角坐标方程及其参数方程;
(2)若把曲线C1上各点的横坐标压缩为原来的$\frac{1}{2}$倍,纵坐标压缩为原来的$\frac{{\sqrt{3}}}{2}$倍,得到曲线C2,设点P是曲线C2上的一个动点,求它到直线l的距离的最小值.
分析 (1)利用极坐标与直角坐标互化的方法,可得曲线C1的直角坐标方程,从而可得参数方程;
(2)点P的坐标是$(\frac{1}{2}cosθ,\frac{{\sqrt{3}}}{2}sinθ)$,从而点P 到直线?的距离是$d=\frac{{|\frac{{\sqrt{3}}}{2}cosθ-\frac{{\sqrt{3}}}{2}sinθ-\sqrt{3}|}}{2}=\frac{{\sqrt{3}}}{4}[\sqrt{2}sin(θ-\frac{π}{4})+2]$,即可求它到直线l的距离的最小值.
解答 解:(1)C1的普通方程为:x2+y2=1.
C1的参数方程为:$\left\{{\begin{array}{l}{x=cosθ}\\{y=sinθ}\end{array}}\right.$(θ为参数).
(2)C2的参数方程为$\left\{{\begin{array}{l}{x=\frac{1}{2}cosθ}\\{y=\frac{{\sqrt{3}}}{2}sinθ}\end{array}}\right.$(θ为参数).故点P的坐标是$(\frac{1}{2}cosθ,\frac{{\sqrt{3}}}{2}sinθ)$,
从而点P 到直线?的距离是$d=\frac{{|\frac{{\sqrt{3}}}{2}cosθ-\frac{{\sqrt{3}}}{2}sinθ-\sqrt{3}|}}{2}=\frac{{\sqrt{3}}}{4}[\sqrt{2}sin(θ-\frac{π}{4})+2]$
由此当$sin(θ-\frac{π}{4})=-1$时,d取得最小值,且最小值为$\frac{{\sqrt{6}}}{4}(\sqrt{2}-1)$.
点评 本题考查极坐标与直角坐标互化,考查参数方程的运用,考查学生的计算能力,属于中档题.

| A. | 2 | B. | $\sqrt{5}$ | C. | 2$\sqrt{5}$ | D. | $\frac{{\sqrt{5}}}{2}$ |
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 无穷多个 |
| A. | $\frac{\sqrt{17}}{2}$ | B. | $\frac{\sqrt{15}}{3}$ | C. | $\frac{\sqrt{57}}{3}$ | D. | $\frac{8}{3}$ |
| A. | $\frac{9}{2}$ | B. | 4 | C. | 3 | D. | 0 |
| A. | 0<e≤$\frac{\sqrt{3}}{2}$ | B. | $\frac{1}{2}$≤e<1 | C. | $\frac{\sqrt{3}}{2}$<e<1 | D. | $\frac{\sqrt{3}}{2}$≤e<1 |
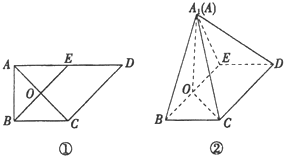 如图①,在直角梯形ABCD中,AD∥BC,∠BAD=$\frac{π}{2}$,AB=BC=$\sqrt{2}$,AD=2$\sqrt{2}$,E是AD的中点,O是AC与BE的交点.将△ABE沿BE折起到△A1BE的位置,如图②.
如图①,在直角梯形ABCD中,AD∥BC,∠BAD=$\frac{π}{2}$,AB=BC=$\sqrt{2}$,AD=2$\sqrt{2}$,E是AD的中点,O是AC与BE的交点.将△ABE沿BE折起到△A1BE的位置,如图②.