题目内容
比较大小：log23 log35．
考点：对数值大小的比较
专题：计算题
分析：根据换底公式得出：log23，log35比较即可．
解答：
解：∵log23=log2
＞log2
=
，log35=log3
＜log3
=
∴log23＞log35．
故答案为：＞
| 9 |
| 8 |
| 3 |
| 2 |
| 25 |
| 27 |
| 3 |
| 2 |
∴log23＞log35．
故答案为：＞
点评：本题考查了换底公式的运用，比较对数的大小，属于中档题．
练习册系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
若函数f（x），g（x）分别是R上的奇函数、偶函数，且满足f（x）-g（x）=ax（a＞1），则有（ ）
| A、f（2）＜f（3）＜g（0） |
| B、g（0）＜f（2）＜g（3） |
| C、f（2）＜g（0）＜f（3） |
| D、g（0）＜f（2）＜f（3） |
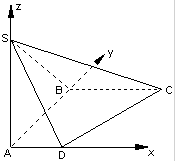已知ABCD为直角梯形，∠DAB=∠ABC=90°，SA⊥平面ABCD，SA=AB=BC=1，AD=