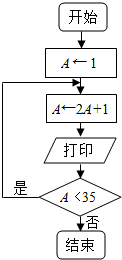
��Ŀ����
15����������{an}����P��ak��=$\frac{1}{k-1}��|{{a_1}-{a_2}}|+|{{a_2}-{a_3}}|+��+|{{a_{k-1}}-{a_k}}|��$������k��2��k��N��Ϊ����{an}��ǰk�������ֵ�������������k��2��k��N������P��ak+1����P��ak�����������{an}Ϊ���������С�����1��������1��x��2Ϊ���������С�����x��ȡֵ��Χ��
��2����֪�Ȳ�����{an}�Ĺ���Ϊd����a1��0��d��0����ǰn��ͼ�ΪSn���Լ��㣺Cn2P��S2��+Cn3P��S3��+��+CnnP��Sn����n��2��n��N����
��3���������Ϊ�����ĵȱ�����{bn}�Ĺ���q�ʣ�0��1������֤��{bn}�ǡ��������С���
���� ��1��������$|{1-x}|��\frac{{|{1-x}|+|{x-2}|}}{2}$���Ӷ������ֵ����ʽ���ɣ�
��2����a1��0��d��0�ɻ���Ϊ$P��{S_k}��=\frac{1}{k-1}��|{a_2}|+|{a_3}|+��+|{a_n}|��={a_1}+\frac{k}{2}d$���Ӷ��õ�$C_n^2P��{S_2}��+C_n^3P��{S_3}��+��+C_n^nP��{S_n}��$=${a_1}��C_n^2+C_n^3+��+C_n^n��$$+\frac{d}{2}��2C_n^2+3C_n^3+��+nC_n^n��$���Ӷ���ã�
��3��${b_n}={b_1}{q^{n-1}}��{b_1}��0��$���Ӷ��жϴ�С��ȥ����ֵ�ţ�����ɵ�$P��{b_{k+1}}��=\frac{{{b_1}��1-q��}}{k}��1+q+{q^2}+��+{q^{k-1}}��$���Ӷ���Ϊk��1+q+q2+��+qk-2������k-1����1+q+q2+��+qk-2+qk-1�����Ӷ�֤����
��� �⣺��1�������⣬$|{1-x}|��\frac{{|{1-x}|+|{x-2}|}}{2}$��
��|1-x|��|x-2|��
��ã�$x��\frac{3}{2}$��
��2��$P��{S_k}��=\frac{1}{k-1}��|{{S_1}-{S_2}}|+|{{S_2}-{S_3}}|+��+|{{S_{k-1}}-{S_k}}|��$=$\frac{1}{k-1}��|{a_2}|+|{a_3}|+��+|{a_n}|��$��
��a1��0��d��0��
��an=a1+��n-1��d��0��
��$P��{S_k}��=\frac{1}{k-1}��|{a_2}|+|{a_3}|+��+|{a_n}|��={a_1}+\frac{k}{2}d$��
��$C_n^2P��{S_2}��+C_n^3P��{S_3}��+��+C_n^nP��{S_n}��$=${a_1}��C_n^2+C_n^3+��+C_n^n��$$+\frac{d}{2}��2C_n^2+3C_n^3+��+nC_n^n��$
=${a_1}��{2^n}-n-1��+$$\frac{d}{2}��nC_{n-1}^1+nC_{n-1}^2+��+nC_{n-1}^{n-1}��$
=${a_1}��{2^n}-n-1��+$$\frac{nd}{2}��{2^n}-1��$��
��3��֤��������֪����${b_n}={b_1}{q^{n-1}}��{b_1}��0��$��
��b1��0��0��q��1���ʶ������k��2��k��N*������bk-1��bk��
���$P��{b_k}��=\frac{1}{k-1}��|{{b_1}-{b_2}}|+|{{b_2}-{b_3}}|+��+|{{b_{k-1}}-{b_k}}|��$
=$\frac{1}{k-1}��{b_1}-{b_2}+{b_2}-{b_3}+��+{b_{k-1}}-{b_k}��=\frac{{{b_1}��1-q��}}{k-1}��1+q+{q^2}+��+{q^{k-2}}��$
$P��{b_{k+1}}��=\frac{{{b_1}��1-q��}}{k}��1+q+{q^2}+��+{q^{k-1}}��$��
��0��q��1��
��qi��qk-1��i��k-1����
��1��qk-1��q��qk-1��q2��qk-1������qk-2��qk-1��
��1+q+q2+��+qk-2����k-1��qk-1��
��k��1+q+q2+��+qk-2������k-1����1+q+q2+��+qk-2+qk-1��
��$\frac{{��1+q+{q^2}+��+{q^{k-2}}��}}{k-1}��\frac{{��1+q+{q^2}+��+{q^{k-2}}+{q^{k-1}}��}}{k}$
��$\frac{{{b_1}��1-q����1+q+{q^2}+��+{q^{k-2}}��}}{k-1}��\frac{{{b_1}��1-q����1+q+{q^2}+��+{q^{k-2}}+{q^{k-1}}��}}{k}$��
���������k��2��k��N*������P��bk����P��bk+1������{bn}�ǡ��������С���
���� ���⿼���˵ȱ�������Ȳ����е�Ӧ�ü�����ʽ������Ӧ�ã�ͬʱ������ѧ���Ļ�������������

| A�� | $[\sqrt{2}-1��\;\sqrt{2}+1]$ | B�� | $[\sqrt{2}-1��\;\sqrt{2}]$ | C�� | $[\sqrt{2}��\;\sqrt{2}+1]$ | D�� | $[2-\sqrt{2}��\;2+\sqrt{2}]$ |
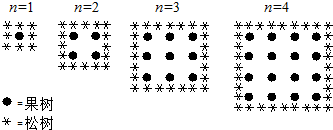 ijũ���滮���������������εij����ڣ�Ϊ�˱������������紵�������ڹ�������Χ�������� ����ͼ�����Կ����滮��ֲ������������n�����������������������Ĺ��ɣ�
ijũ���滮���������������εij����ڣ�Ϊ�˱������������紵�������ڹ�������Χ�������� ����ͼ�����Կ����滮��ֲ������������n�����������������������Ĺ��ɣ�