题目内容
4．流程图（如图）的打印结果是3 7 15 31 63．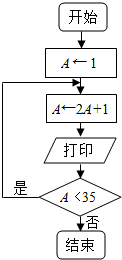
分析 由已知中的程序框图可知：该程序的功能是利用循环结构计算并输出变量A的值，模拟程序的运行过程，分析循环中各变量值的变化情况，可得答案．
解答 解：第一次执行循环体，A=3，打印3后，满足继续循环的条件；
第二次执行循环体，A=7，打印7后，满足继续循环的条件；
第三次执行循环体，A=15，打印15后，满足继续循环的条件；
第四次执行循环体，A=31，打印31后，满足继续循环的条件；
第五次执行循环体，A=63，打印63后，不满足继续循环的条件；
故打印的结果是：3 7 15 31 63；
故答案为：3 7 15 31 63
点评 本题考查的知识点是程序框图，当循环的次数不多，或有规律时，常采用模拟循环的方法解答．
练习册系列答案
阅读快车系列答案
相关题目
12．如表示采集的商品零售额（万元）与商品流通费率的一组数据：
（1）将商品零售额作为横坐标，商品流通费率作为纵坐标，在平面直角坐标系内作出散点图；
（2）商品零售额与商品流通费率具有线性相关关系吗？如果商品零售额是20万元，那么能否预测此时流通费率是多少呢？（b=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{xy}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$ a=$\overline{y}$-b$\overline{x}$）
| 商品零售额 | 9.5 | 11.5 | 13.5 | 15.5 | 17.5 | 19.5 | 21.5 | 23.5 | 25.5 | 27.5 |
| 商品流通费率 | 6.0 | 4.6 | 4.0 | 3.2 | 2.8 | 2.5 | 2.4 | 2.3 | 2.2 | 2.1 |
（2）商品零售额与商品流通费率具有线性相关关系吗？如果商品零售额是20万元，那么能否预测此时流通费率是多少呢？（b=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{xy}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$ a=$\overline{y}$-b$\overline{x}$）
19．一束光线从点P（-1，1）出发，经x轴反射到圆C：（x-2）2+（y-3）2=1上一点的最长路程是（ ）
| A． | 3$\sqrt{2}$-1 | B． | 2$\sqrt{6}$ | C． | 5 | D． | 6 |
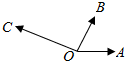如图所示，|$\overrightarrow{OA}$|=|$\overrightarrow{OB}$|=1，|$\overrightarrow{OC}$|=$\sqrt{3}$，∠AOB=60°，$\overrightarrow{OB}$⊥$\overrightarrow{OC}$．若$\overrightarrow{OC}$=x$\overrightarrow{OA}$+y$\overrightarrow{OB}$，则x，y的值分别是（ ）