题目内容
方程|x+1|=2x根的个数为( )
| A、0 | B、1 | C、2 | D、3 |
考点:根的存在性及根的个数判断
专题:函数的性质及应用
分析:方程|x+1|=2x根的个数,即为函数y=|x+1|与y=2x图象交点的个数,画出两个函数的图象,可得答案.
解答:
解:方程|x+1|=2x根的个数,即为函数y=|x+1|与y=2x图象交点的个数,
在同一坐标系中画出函数y=|x+1|与y=2x图象如下图所示:

由图可得:函数y=|x+1|与y=2x图象有且只有三个交点,
故方程|x+1|=2x根的个数为3个,
故选:D
在同一坐标系中画出函数y=|x+1|与y=2x图象如下图所示:

由图可得:函数y=|x+1|与y=2x图象有且只有三个交点,
故方程|x+1|=2x根的个数为3个,
故选:D
点评:本题考察了函数的根的存在性问题,渗透了转化思想,是一道基础题.

练习册系列答案
相关题目
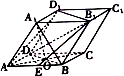 如图,四棱柱ABCD-A1B1C1D1的底面ABCD是正方形,O为底面中心,E是AB的中点,A1O=1,A1B=AB=AA1=
如图,四棱柱ABCD-A1B1C1D1的底面ABCD是正方形,O为底面中心,E是AB的中点,A1O=1,A1B=AB=AA1=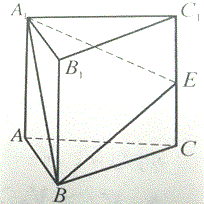 正三棱柱ABC-A1B1C1中,所有棱长都是4,E是CC1的中点.
正三棱柱ABC-A1B1C1中,所有棱长都是4,E是CC1的中点.