题目内容

一个袋中装有3个红球和3个白球，现从袋中取出1球，然后放回袋中再取出一球，则取出的两个球是同色球的概率是（　　）
A、
1
2
B、
1
3
C、
1
6
D、
1
9
考点：古典概型及其概率计算公式
专题：概率与统计
分析：易得总的方法种数为36，符合题意的共18种，由概率公式可得．
解答： 解：因为是有放回的抽取，所以总的方法种数共6×6=36，
其中取出的两个球是同色球的共3×3+3×3=18，
故所求概率为P=
18
36
=
1
2

故选：A
点评：本题考查古典概型及其概率公式，属基础题．
练习册系列答案
相关题目
方程sin2x=sin3x的解集是
 
．
举世瞩目的巴西足球世界杯将于2014年6月在巴西举行，这是四年一度的足球盛宴，是全世界足球迷的节日．在每场比赛之前，世界杯组委会都会指派裁判员进行执法．在某场比赛前，有10名裁判可供选择，其中欧洲裁判3人，亚洲裁判4人，美洲裁判3人．若组委会要从这10名裁判中任选3人执法本次比赛．求：
（1）选出的欧洲裁判人数多于亚洲裁判人数的概率；
（2）选出的3人中，欧洲裁判人数X的分布列和数学期望．
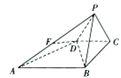如图所示，已知四棱锥P=ABCD的底面是直角梯形，∠ABC=∠BCD=90°，AB=BC=PB=PC=2，CD=1，侧面PBC⊥底面ABCD，点F在线段AP上，且满足PF=λPA．
（Ⅰ）当λ=
1
2
时，求证：DF∥平面PBC；
（Ⅱ）当λ=
1
3
时，求三棱锥F-PCD的体积．
一张坐标纸对折一次后，点A（0，4）与点B（8，0）重叠，则折痕所在直线与两坐标轴围成的面积是
 
．
将a、b、c、d四个小球放入三个不同盒子，每个盒子至少放一个，且a、b不在同一个盒子中的方法有
 
种．
已知双曲线C：
x2
a2
-
y2
b2
=1的右焦点为F，过F作双曲线C的一条渐近线的垂线，垂足为H，交双曲线C于点M，|FM|=|HM|，则双曲线C的离心率为（　　）
A、2
B、
3
C、
6
2
D、
2
下列命题：
①三角形ABC中，若a2+b2-c2-ab=0，则C=60°；
②ax（x-1）＜0（a≠0）的解集是（0，1）；
③Sn是数列{an}的前n项和，若Sn=n2+1，则an=2n-1；
④Sn是数列{an}的前n项和，若Sn=2n-1，则数列{an}是等比数列．
其中正确命题的序号是：
 
．
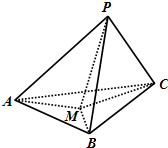如图，在三棱锥P-ABC中，PA、PB、PC两两互相垂直，且PA=3，PB=2，PC=1，设M是底面ABC内一点，定义f（M）=（m，n，p），其中m，n，p分别是三棱锥M-PAB、三棱锥M-PBC、三棱锥M-PCA的体积，若f（M）=（
1
2
，x，y），且
1
x
+
a
y
≥8恒成立，则正实数a的最小值为
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网