题目内容
如图,四边形ABCD是正方形,E是AD上一点,且AE=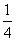 AD,N是AB的中点,
AD,N是AB的中点,
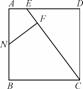
NF⊥CE于F,求证:FN2=EF·FC.
证明:连结NC、NE,设正方形的边长为a,
∵ AE=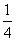 a,AN=
a,AN=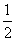 a,∴ NE=
a,∴ NE= a.
a.
∵ BN=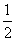 a,BC=a,∴ NC=
a,BC=a,∴ NC= a.
a.
∵ DE=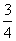 a,DC=a,∴ EC=
a,DC=a,∴ EC= a.
a.
又NE2= a2,NC2=
a2,NC2= a2,EC2=
a2,EC2= a2,
a2,
且NE2+NC2=EC2,∴ EN⊥NC.
∵ NF⊥CE,∴ FN2=EF·FC.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案
相关题目
 的特征值及相应的特征向量.
的特征值及相应的特征向量.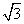 sinθ)=2的距离为d.求d的最大值.
sinθ)=2的距离为d.求d的最大值.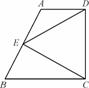

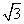 ,OA=
,OA=
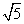 ,C是圆O外一点,AC交圆O于点E,BC交圆O于点D,已知AC=AB,BC=4,求△ADE的周长.
,C是圆O外一点,AC交圆O于点E,BC交圆O于点D,已知AC=AB,BC=4,求△ADE的周长.
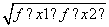 =C,则称函数f(x)在D上的几何平均数为C.已知f(x)=x3,x∈[1,2],则函数f(x)=x3在[1,2]上的几何平均数为( )
=C,则称函数f(x)在D上的几何平均数为C.已知f(x)=x3,x∈[1,2],则函数f(x)=x3在[1,2]上的几何平均数为( ) B.2
B.2