题目内容
如图，在梯形ABCD中，AD∥BC，∠ADC＝90°，E是AB边的中点，求证：ED＝EC.
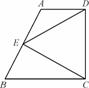
证明： 如图，过E点作EF∥BC交DC于点F.在梯形ABCD中，AD∥BC，
∴ AD∥EF∥BC.
∵ E是AB的中点，
∴ F是DC的中点．
∵ ∠ADC＝90°，
∴ ∠DFE＝90°.
∴ EF是DC的垂直平分线，
∴ ED＝EC.
练习册系列答案
开心蛙状元作业系列答案
课时掌控随堂练习系列答案
一课一练一本通系列答案
浙江之星学业水平测试系列答案
相关题目
)，求△OAB在矩阵MN的作用下变换所得到的图形的面积，其中矩阵M＝
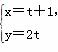(t为参数)，曲线C的参数方程为
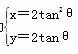(θ为参数)，试求直线l与曲线C的普通方程，并求出它们的公共点的坐标．
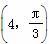，求|CP|.
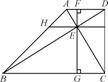
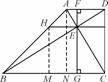
AD，N是AB的中点，
