题目内容
在极坐标系中，设圆ρ＝3上的点到直线ρ(cosθ＋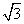
sinθ)＝2的距离为d.求d的最大值．
解：将极坐标方程ρ＝3化为普通方程，得圆：x2＋y2＝9.
极坐标方程ρ(cosθ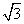＋sinθ)＝2化为普通方程，得直线：x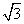＋y＝2.
在x2＋y2＝9上任取一点A(3cosα，3sinα)．
则点A到直线的距离为d＝
∴ 所求d的最大值为4.
练习册系列答案
相关题目
题目内容
在极坐标系中，设圆ρ＝3上的点到直线ρ(cosθ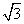＋sinθ)＝2的距离为d.求d的最大值．
解：将极坐标方程ρ＝3化为普通方程，得圆：x2＋y2＝9.
极坐标方程ρ(cosθ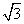＋sinθ)＝2化为普通方程，得直线：x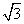＋y＝2.
在x2＋y2＝9上任取一点A(3cosα，3sinα)．
则点A到直线的距离为d＝
∴ 所求d的最大值为4.
，求二阶方阵X，使MX＝N.
(t为参数)，曲线C的参数方程为
(θ为参数)，试求直线l与曲线C的普通方程，并求出它们的公共点的坐标．
，求|CP|.
AD，N是AB的中点，
≤k恒成立，求k的取值范围．