题目内容
14.已知直线l经过点P(-2,5),且斜率为$-\frac{3}{4}$,若直线m与l平行且两直线间的距离为3,则直线m的方程为3x+4y+1=0,或 3x+4y-29=0.分析 由直线m与直线l平行,可设直线m的方程为3x+4y+c=0,由点到直线的距离公式求得待定系数c 值,即得所求直线方程.
解答 解:由直线m与直线l平行,可设直线m的方程为3x+4y+c=0,
∵直线m与l平行且两直线间的距离为3,
∴点P到直线m的距离为3,由点到直线的距离公式,得$\frac{|-6+20+c|}{5}$=3,
解得c=1或c=-29,故所求直线方程 3x+4y+1=0,或 3x+4y-29=0.
故答案为:3x+4y+1=0,或 3x+4y-29=0.
点评 本题考查用待定系数法求直线的方程,点到直线的距离公式的应用,求出待定系数是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
4. 一线性规划问题的可行域为坐标平面上的正八边形ABCDEFGH及其内部(如图),已知目标函数z=3+ax+by(a,b∈R)的最大值只在顶点B处,如果目标函数变成z=3-bx-ay时,最大值只在顶点( )
一线性规划问题的可行域为坐标平面上的正八边形ABCDEFGH及其内部(如图),已知目标函数z=3+ax+by(a,b∈R)的最大值只在顶点B处,如果目标函数变成z=3-bx-ay时,最大值只在顶点( )
 一线性规划问题的可行域为坐标平面上的正八边形ABCDEFGH及其内部(如图),已知目标函数z=3+ax+by(a,b∈R)的最大值只在顶点B处,如果目标函数变成z=3-bx-ay时,最大值只在顶点( )
一线性规划问题的可行域为坐标平面上的正八边形ABCDEFGH及其内部(如图),已知目标函数z=3+ax+by(a,b∈R)的最大值只在顶点B处,如果目标函数变成z=3-bx-ay时,最大值只在顶点( )| A. | A | B. | B | C. | C | D. | D |
2.如图,网格纸上小正方形的边长为1,粗线画出的是某三棱锥的三视图,则该三棱锥的表面积是( )


| A. | $1+\sqrt{5}$ | B. | $2+\sqrt{5}$ | C. | $1+2\sqrt{5}$ | D. | $2+2\sqrt{5}$ |
9.设复数z满足|z-3-4i|=1,其中i为虚数单位,则|z|的最大值是( )
| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
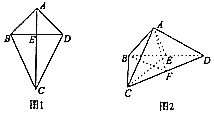 如图1,四边形ABCD中AC⊥BD,CE=2AE=2BE=2DE=2,将四边形ABCD沿着BD折叠,得到图2所示的三棱锥A-BCD,其中AB⊥CD.
如图1,四边形ABCD中AC⊥BD,CE=2AE=2BE=2DE=2,将四边形ABCD沿着BD折叠,得到图2所示的三棱锥A-BCD,其中AB⊥CD.