题目内容
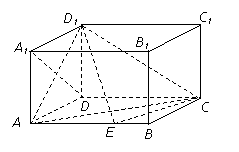
如图,在长方体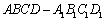 中,
中,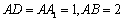 ,点
,点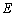 是棱AB上的一个动点 .
是棱AB上的一个动点 .
(Ⅰ)证明: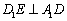 ;
;
(Ⅱ)当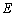 为
为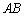 的中点时,求点
的中点时,求点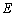 到面
到面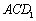 的距离;
的距离;
(Ⅲ)线段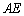 的长为何值时,二面角
的长为何值时,二面角 的大小为
的大小为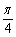 .
.
 |
解法一
(Ⅰ)∵ 平面
平面 ,∴
,∴ ,又∵
,又∵ ,
,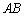 ∩
∩ ,∴
,∴ 平面
平面 ,
,
 .
.
(Ⅱ)等体积法
由已知条件可得, ,
, ,所以
,所以 为等腰三角形,
为等腰三角形,

 =
= ,
, 
 ,设点
,设点 到平面
到平面 的距离
的距离 ,根据
,根据 可得,
可得, ,即
,即 ,
,
解得 .
.
(Ⅲ)过点 作
作 于
于 ,连接
,连接 .
.
因为 平面
平面 ,所以
,所以
 ,又
,又 ,
, ∩
∩ ,所以
,所以 平面
平面 ,
,
故
 ,
, 为二面角
为二面角 的平面角,所以
的平面角,所以 ,
,
 ,
,
 ,
, ,
, ,由
,由 可得
可得 ,
, .
.
解法二:以 为坐标原点,直线
为坐标原点,直线 分别为
分别为 轴,建立空间直角坐标系,
轴,建立空间直角坐标系,
设 ,则
,则


(I) 因为 所以
所以 ,即
,即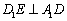 .
.
(II) (II)因为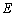 为
为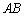 的中点,则
的中点,则 ,从而
,从而 ,
,
 ,设平面
,设平面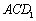 的法向量为
的法向量为 ,则
,则
也即 ,得
,得 , 设
, 设 ,从而
,从而 ,所以点
,所以点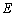 到平面
到平面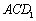 的距离为
的距离为

(Ⅲ)设平面 的法向量
的法向量 ,
,
∴
由 令
令 ,
,
∴
依题意
∴ (不合,舍去),
(不合,舍去), .
.
∴ 时,二面角
时,二面角 的大小为
的大小为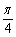

练习册系列答案
相关题目
 满足:
满足: .
.  项和
项和 ;
; 的前
的前 ,且
,且 ,求
,求 是偶函数,则
是偶函数,则 _______.
_______. (B)
(B) (C)
(C) (D)
(D)

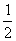 DC,
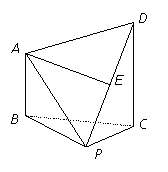
DC, .
.

 的解集为
的解集为  的值域为
的值域为 ,若关于
,若关于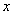 的不等式
的不等式 的解集为
的解集为 ,则实数
,则实数 的值为 .
的值为 . 的解集中的整数有且仅有1,2,3
的解集中的整数有且仅有1,2,3 ,则
,则 的取值范围 .
的取值范围 .