题目内容
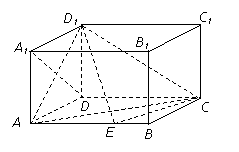
如图,在四棱锥P-ABCD中,△PBC为正三角形,AB⊥平面PBC,AB∥DC,AB=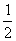 DC,
DC,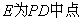 .
.
(Ⅰ)求证:AE∥平面PBC;
(Ⅱ)求证:AE⊥平面PDC.
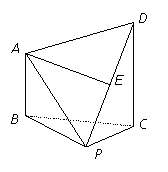
解(Ⅰ)证明:取PC的中点M,连接EM、BM,
则EM∥CD,EM=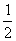 DC,
DC,

 EM∥AB且EM=AB,则四边形ABME是平行四边形.
EM∥AB且EM=AB,则四边形ABME是平行四边形.
 AE∥BM,
AE∥BM, AE
AE 平面PBC内,
平面PBC内,
 AE∥平面PBC.
AE∥平面PBC.
(Ⅱ) 因为AB⊥平面PBC,AB∥CD,
所以CD⊥平面PBC,CD⊥BM.
由(1)得,BM⊥PC,所以BM⊥平面PDC,又AE∥BM,
所以AE⊥平面PDC.

练习册系列答案
相关题目
 (
( 是虚数单位),则
是虚数单位),则 .
. 与
与 的图像不具有下述哪种性质
的图像不具有下述哪种性质 个单位后,与
个单位后,与 互相对称
互相对称 上都为增函数
上都为增函数 (B)
(B) (C)
(C) (D)
(D)
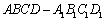 中,
中,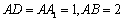 ,点
,点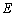 是棱AB上的一个动点 .
是棱AB上的一个动点 .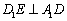 ;
; 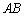 的中点时,求点
的中点时,求点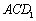 的距离;
的距离; 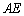 的长为何值时,二面角
的长为何值时,二面角 的大小为
的大小为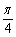 .
.
 表示的平面区域内运动,则z=x-y的取值范围是( )
表示的平面区域内运动,则z=x-y的取值范围是( ) 中,若
中,若 ,
, ,
, ,则三角形
,则三角形 的面积
的面积 ________.
________. 有解,则整数
有解,则整数 的值只能有( )
的值只能有( )