题目内容
在等差数列{an}中,d=2,S20=60,则S21等于( )
| A、62 | B、64 | C、84 | D、100 |
考点:等差数列的前n项和
专题:等差数列与等比数列
分析:由已知条件利用等差数列的前n项和公式能求出首项,由此能求出S21.
解答:
解:∵在等差数列{an}中,d=2,S20=60,
∴20a1+
×2=60,
解得a1=-16,
∴S21=21×(-16)+
×2=84.
故选:C.
∴20a1+
| 20×19 |
| 2 |
解得a1=-16,
∴S21=21×(-16)+
| 21×20 |
| 2 |
故选:C.
点评:本题考查等差数列的前21项和的求法,是基础题,解题时要认真审题,注意等差数列的性质的合理运用.

练习册系列答案
 英才计划期末调研系列答案
英才计划期末调研系列答案 精英口算卡系列答案
精英口算卡系列答案
相关题目
已知m>0,n>0,且2m,
,3n成等差数列,则
+
的最小值为( )
| 5 |
| 2 |
| 2 |
| m |
| 3 |
| n |
A、
| ||
| B、5 | ||
C、
| ||
| D、15 |
设 a=
,b=
,c=
,则a,b,c的大小关系为( )
| e4 |
| 16 |
| e5 |
| 25 |
| e6 |
| 36 |
| A、a>b>c |
| B、b>a>c |
| C、c>b>a |
| D、c>a>b |
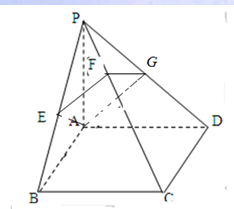 如图PA⊥正方ABCD所在平面,经过A且垂直于PC的平面分别交PB、PC、PD于E、F、G求证:AE⊥PB.
如图PA⊥正方ABCD所在平面,经过A且垂直于PC的平面分别交PB、PC、PD于E、F、G求证:AE⊥PB.