题目内容
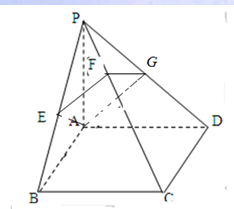 如图PA⊥正方ABCD所在平面,经过A且垂直于PC的平面分别交PB、PC、PD于E、F、G求证:AE⊥PB.
如图PA⊥正方ABCD所在平面,经过A且垂直于PC的平面分别交PB、PC、PD于E、F、G求证:AE⊥PB.考点:空间中直线与直线之间的位置关系
专题:证明题,空间位置关系与距离
分析:运用线面垂直的性质和判定定理,以及正方形的定义,注意转化思想的运用,即可得证.
解答:
证明:PA⊥正方ABCD所在平面,
则PA⊥BC,
又正方形ABCD中,BC⊥AB,
则BC⊥平面PAB,且AE?平面PAB,
则BC⊥AE,
又PC⊥平面AEFG,
则PC⊥AE,
则AE⊥平面PBC,
则有AE⊥PB.
则PA⊥BC,
又正方形ABCD中,BC⊥AB,
则BC⊥平面PAB,且AE?平面PAB,
则BC⊥AE,
又PC⊥平面AEFG,
则PC⊥AE,
则AE⊥平面PBC,
则有AE⊥PB.
点评:本题考查直线和平面垂直的性质和判定定理及运用,考查转化和推理能力,属于基础题.

练习册系列答案
相关题目
在等差数列{an}中,d=2,S20=60,则S21等于( )
| A、62 | B、64 | C、84 | D、100 |
下列函数中值域为R的函数有( )
①y=(
)x ②y=x2 ③y=
④y=log2x.
①y=(
| 1 |
| 2 |
| 1 |
| x |
| A、1个 | B、2个 | C、3个 | D、4个 |
如果变量x,y满足约束条件
,则
的取值范围是( )
|
| 2y-2x-2 |
| 2x+1 |
A、[
| ||||
B、(-∞,
| ||||
C、(-∞,
| ||||
D、[
|
设f(x)=
,则f(f(
))=( )
|
| 10 |
| A、e | B、1 | C、2 | D、以上都不对 |
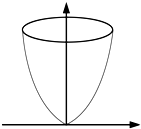 抛物线y=x2(-2≤x≤2)绕y轴旋转一周形成一个如图所示的旋转体,在此旋转体内水平放入一个正方体,使正方体的一个面恰好与旋转体的开口面平齐,则此正方体的棱长是
抛物线y=x2(-2≤x≤2)绕y轴旋转一周形成一个如图所示的旋转体,在此旋转体内水平放入一个正方体,使正方体的一个面恰好与旋转体的开口面平齐,则此正方体的棱长是