题目内容
设y=f(x)+2x为奇函数,且g(x)=f(x)+2,若g(-2)=t,则f(2)= .(用含t的代数式表示)
考点:函数解析式的求解及常用方法
专题:函数的性质及应用
分析:根据题意得出f(-x)+2-x=-f(x)-2x;x=2时,f(-2)+2-2=-f(2)-22,运用g(-2)=t求出f(-2)即可.
解答:
解:∵y=f(x)+2x为奇函数,
∴f(-x)+2-x=-f(x)-2x,
∵g(x)=f(x)+2,
g(-2)=t
∴f(-2)+2=t,f(-2)=t-2,
∴f(-2)+2-2=-f(2)-22,
即t-2+
=-f(2)-4,
f(2)=-t-
,
故答案为:-t-
,
∴f(-x)+2-x=-f(x)-2x,
∵g(x)=f(x)+2,
g(-2)=t
∴f(-2)+2=t,f(-2)=t-2,
∴f(-2)+2-2=-f(2)-22,
即t-2+
| 1 |
| 4 |
f(2)=-t-
| 9 |
| 4 |
故答案为:-t-
| 9 |
| 4 |
点评:本题综合考察了函数的性质,方程的运用,注意符号的书写,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
△ABC中,A=
,BC=
,AC=
,则角B等于( )
| π |
| 3 |
| 3 |
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
在等差数列{an}中,d=2,S20=60,则S21等于( )
| A、62 | B、64 | C、84 | D、100 |
下列函数中值域为R的函数有( )
①y=(
)x ②y=x2 ③y=
④y=log2x.
①y=(
| 1 |
| 2 |
| 1 |
| x |
| A、1个 | B、2个 | C、3个 | D、4个 |
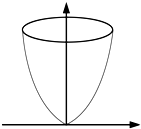 抛物线y=x2(-2≤x≤2)绕y轴旋转一周形成一个如图所示的旋转体,在此旋转体内水平放入一个正方体,使正方体的一个面恰好与旋转体的开口面平齐,则此正方体的棱长是
抛物线y=x2(-2≤x≤2)绕y轴旋转一周形成一个如图所示的旋转体,在此旋转体内水平放入一个正方体,使正方体的一个面恰好与旋转体的开口面平齐,则此正方体的棱长是