题目内容
函数f（x）=cos（2x+
）的最小正周期是（ ）
| π |
| 4 |
A、
| ||
| B、π | ||
| C、2π | ||
| D、4π |
考点：三角函数的周期性及其求法
专题：三角函数的图像与性质
分析：由题意得ω=2，再代入复合三角函数的周期公式T=
求解．
| 2π |
| |ω| |
解答：
解：根据复合三角函数的周期公式T=
得，
函数f（x）=cos（2x+
）的最小正周期是π，
故选：B．
| 2π |
| |ω| |
函数f（x）=cos（2x+
| π |
| 4 |
故选：B．
点评：本题考查了三角函数的周期性，以及复合三角函数的周期公式T=
应用，属于基础题．
| 2π |
| |ω| |
练习册系列答案
习题精选系列答案
相关题目
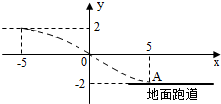如图，某飞行器在4千米高空飞行，从距着陆点A的水平距离10千米处开始下降，已知下降飞行轨迹为某三次函数图象的一部分，则该函数的解析式为（ ）A、y=
| ||||
B、y=
| ||||
C、y=
| ||||
D、y=-
|
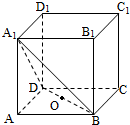如图，在正方体ABCD-A1B1C1D1中，点O为线段BD的中点，设点P在线段CC1上，直线OP与平面A1BD所成的角为α，则sinα的取值范围是（ ）A、[
| ||||||||
B、[
| ||||||||
C、[
| ||||||||
D、[
|
复数z=（3-2i）i的共轭复数
等于（ ）
. |
| z |
| A、-2-3i | B、-2+3i |
| C、2-3i | D、2+3i |
已知全集U=R，A={x|x≤0}，B={x|x≥1}，则集合∁U（A∪B）=（ ）
| A、{x|x≥0} |
| B、{x|x≤1} |
| C、{x|0≤x≤1} |
| D、{x|0＜x＜1} |
设命题p：?x∈R，x2+1＞0，则￢p为（ ）
| A、?x0∈R，x02+1＞0 |
| B、?x0∈R，x02+1≤0 |
| C、?x0∈R，x02+1＜0 |
| D、?x∈R，x2+1≤0 |