Question

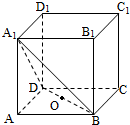如图，在正方体ABCD-A₁B₁C₁D₁中，点O为线段BD的中点，设点P在线段CC₁上，直线OP与平面A₁BD所成的角为α，则sinα的取值范围是（　　）

• A、[

  3

  3

  ，1]
• B、[

  6

  3

  ，1]
• C、[

  6

  3

  ，

  2 2

  3

  ]
• D、[

  2 2

  3

  ，1]

Answer 1

考点：直线与平面所成的角

专题：空间角

分析：由题意可得：直线OP于平面A₁BD所成的角α的取值范围是[∠AOA1，

π

2

]∪[∠C1OA1，

π

2

]．再利用正方体的性质和直角三角形的边角关系即可得出．

解答： 解：由题意可得：直线OP于平面A₁BD所成的角α的取值范围是[∠AOA1，

π

2

]∪[∠C1OA1，

π

2

]．
不妨取AB=2．
在Rt△AOA₁中，sin∠AOA1=

AA1

A1O

=

2

22+( 2 )2

=

6

3

．
sin∠C₁OA₁=sin（π-2∠AOA₁）=sin2∠AOA₁=2sin∠AOA₁cos∠AOA₁=2×

6

3

×

3

3

=

2 2

3

＞

6

3

，
sin

π

2

=1．
∴sinα的取值范围是[

6

3

，1]．
故选：B．

点评：本题考查了正方体的性质和直角三角形的边角关系即可、线面角的求法，考查了推理能力，属于中档题．