题目内容
6.如图,有一正三角形铁皮余料,欲利用余料剪裁出一个矩形(矩形的一个边在三角形的边上),并以该矩形制作一铁皮圆柱的侧面.问:如何剪裁,才能使得铁皮圆柱的体积最大?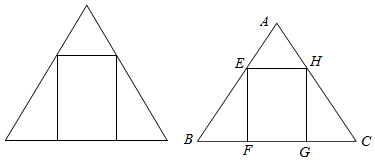
分析 假设正三角形边长为a,EF=x,用x表示出GF,分两种情况计算圆柱的体积V(x),利用导数与函数最值得关系求出V(x)的极大值和极大值点,得出结论.
解答 解:设正三角形长为a,设EF=x,则BF=$\frac{x}{\sqrt{3}}$,GF=a-$\frac{2x}{\sqrt{3}}$.
(1)若以EF为底、GF为高,则圆柱底面半径r=$\frac{x}{2π}$,
V(x)=πr2•GF=π($\frac{x}{2π}$)2(a-$\frac{2x}{\sqrt{3}}$)=$\frac{1}{4π}$(ax2-$\frac{2{x}^{3}}{\sqrt{3}}$),0<x<$\frac{\sqrt{3}a}{2}$.
∴V′=$\frac{1}{4π}$(2ax-2$\sqrt{3}$x2)=-$\frac{x}{2π}$($\sqrt{3}$x-a).
当0<x<$\frac{a}{\sqrt{3}}$时,V′>0;当$\frac{a}{\sqrt{3}}$<x<$\frac{\sqrt{3}a}{2}$时,V′<0;
∴当x=$\frac{a}{\sqrt{3}}$时,V(x)取得最小值V($\frac{a}{\sqrt{3}}$)=$\frac{{a}^{3}}{36π}$.
(2)若以GF为底、EF为高,则圆柱底面半径r=$\frac{a-\frac{2x}{\sqrt{3}}}{2π}$.
V(x)=πr2•EF=π($\frac{a-\frac{2x}{\sqrt{3}}}{2π}$)2x=$\frac{1}{4π}$($\frac{4{x}^{3}}{3}$-$\frac{4a{x}^{2}}{\sqrt{3}}$+a2x),0<x<$\frac{\sqrt{3}a}{2}$.
V′(x)=$\frac{1}{4π}$(4x2-$\frac{8ax}{\sqrt{3}}$+a2),
令V′(x)=0,得x1=$\frac{a}{2\sqrt{3}}$、x2=$\frac{\sqrt{3}a}{2}$.
当0<x<$\frac{a}{2\sqrt{3}}$时,V′(x)>0;当$\frac{a}{2\sqrt{3}}$<x<$\frac{\sqrt{3}a}{2}$时,V′(x)<0;
∴当x=$\frac{a}{2\sqrt{3}}$时,V(x)取得最大值V($\frac{a}{2\sqrt{3}}$)=$\frac{{a}^{3}}{18\sqrt{3}π}$.
∵$\frac{{a}^{3}}{18\sqrt{3}π}$>$\frac{{a}^{3}}{36π}$,
∴以GF为底、EF为高,且EF=$\frac{a}{2\sqrt{3}}$时,体积最大.
点评 本题考查了圆柱的结构特征,利用导数求函数的极值,属于中档题.

 华东师大版一课一练系列答案
华东师大版一课一练系列答案 孟建平名校考卷系列答案
孟建平名校考卷系列答案| A. | a | B. | b | C. | $\frac{a}{2}$ | D. | $\frac{b}{2}$ |
| A. | ($\frac{1+\sqrt{5}}{2},+∞$) | B. | ($\frac{1+\sqrt{5}}{2},2$) | C. | (2,+∞) | D. | (1,$\frac{1+\sqrt{5}}{2}$) |
| A. | $\frac{\sqrt{3}}{5}$ | B. | $\frac{2\sqrt{3}}{3}$ | C. | $\frac{4\sqrt{3}}{3}$ | D. | $\frac{5\sqrt{3}}{3}$ |
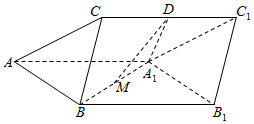 如图,三棱柱ABC-A1B1C1中,D,M分别为CC1和A1B的中点,A1D⊥CC1,侧面ABB1A1为菱形且∠BAA1=60°,AA1=A1D=2,BC=1,
如图,三棱柱ABC-A1B1C1中,D,M分别为CC1和A1B的中点,A1D⊥CC1,侧面ABB1A1为菱形且∠BAA1=60°,AA1=A1D=2,BC=1,