题目内容

已知△ABC中，BC边上的中线AO长为2，若动点P满足
BP
=
1
2
cos2θ 
BC
+sin2θ 
BA
（θ∈R），则（
PB
+
PC
）•
PA
的最小值是
 
．
考点：平面向量数量积的运算
专题：平面向量及应用
分析：由题意可得点P在AO上，
PB
+
PC
=2
PO
，故有（
PB
+
PC
）•
PA
=2
PO
•
PA
=-2|
PO
|•|
PA
|．根据|
PO
|+|
PA
|=|AO|=2，利用基本不等式可得|
PO
|•|
PA
|的最大值，可得要求式子的最小值．
解答： 解：由题意可得
BC
=2
BO
，∵点P满足
BP
=
1
2
cos2θ 
BC
+sin2θ 
BA
（θ∈R），
∴
BP
= cos2θ 
BO
+sin2θ 
BA
．
又sin2θ+cos2θ=1，所以P、A、O三点共线，即点P在AO上．
∵
PB
+
PC
=2
PO
，∴（
PB
+
PC
）•
PA
=2
PO
•
PA
=-2|
PO
|•|
PA
|．
∴|
PO
|+|
PA
|=|AO|=2，利用基本不等式可得|
PO
|•|
PA
|≤(
|
PO
|+|
PA
|
2
)2=1，
∴-2|
PO
|•|
PA
|≥-2，当且仅当|PO|=|PA|时，等号成立，
故（
PB
+
PC
）•
PA
的最小值为-2，
故答案为：-2．
点评：本题考查向量的数量积的运算和基本不等式的应用，由题意得出P、M、C三点共线是解决问题的关键，属中档题．
练习册系列答案
相关题目
直线l：y=x+4与圆x2+y2-3y-1=0有
 
个公共点．
与直线2x-y+4=0关于x轴对称的直线方程是
 
．
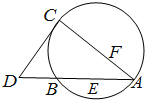如图，CD为△ABC外接圆的切线，AB的延长线交直线CD于点D，E，F分别为弦AB与弦AC上的点，且BC•AE=DC•AF，B，E，F，C四点共圆．若DB=BE=EA，则过B，E，F，C四点的圆的面积与△ABC外接圆面积的比值为
 
．
若数列{an}的前n项和Sn=n2-n+1，则an=
 
．
b克糖水中有a克糖（b＞a＞0），若在糖水中再放上m（m＞0）克糖，则糖水变得更甜了．根据这一事实可提炼出的不等式是
 
．
已知命题p：方程
x2
m
+
y2
m-2
=1表示的曲线为椭圆；命题q：方程
x2
m-1
+
y2
m-3
=1表示的曲线为双曲线；若p或q为真，p且q为假，则实数的取值范围为
 
．
以下程序运行后的输出结果为（　　）
A、21B、13C、17D、25
已知函数f(x)=log2x，f(
1
4
)等于（　　）
A、-1B、-2C、2D、3

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网