题目内容
函数y=lg(ax2-x+1)的值域为R,则a的取值范围是 .
考点:对数函数的值域与最值
专题:函数的性质及应用
分析:根据对数函数的性质建立条件关系即可得到结论.
解答:
解:∵函数y=lg(ax2-x+1)的值域为R,
∴ax2-x+1能取遍所有的正数,
设f(x)=ax2-x+1,
即(0,+∞)?{y|y=f(x)},
当a=0时,f(x)=ax2-x+1=-x+1,满足条件.
当a≠0,要使f(x)=ax2-x+1满足条件,
则当a<0,不满足条件,
当a>0时,则满足判别式△=1-4a≥0,
即0<a≤
.
综上0≤a≤
.
故答案为:0≤a≤
.
∴ax2-x+1能取遍所有的正数,
设f(x)=ax2-x+1,
即(0,+∞)?{y|y=f(x)},
当a=0时,f(x)=ax2-x+1=-x+1,满足条件.
当a≠0,要使f(x)=ax2-x+1满足条件,
则当a<0,不满足条件,
当a>0时,则满足判别式△=1-4a≥0,
即0<a≤
| 1 |
| 4 |
综上0≤a≤
| 1 |
| 4 |
故答案为:0≤a≤
| 1 |
| 4 |
点评:本题主要考查对数函数的性质和应用,注意定义域为R和值域为R的区别和联系.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
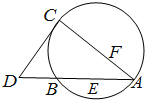 如图,CD为△ABC外接圆的切线,AB的延长线交直线CD于点D,E,F分别为弦AB与弦AC上的点,且BC•AE=DC•AF,B,E,F,C四点共圆.若DB=BE=EA,则过B,E,F,C四点的圆的面积与△ABC外接圆面积的比值为
如图,CD为△ABC外接圆的切线,AB的延长线交直线CD于点D,E,F分别为弦AB与弦AC上的点,且BC•AE=DC•AF,B,E,F,C四点共圆.若DB=BE=EA,则过B,E,F,C四点的圆的面积与△ABC外接圆面积的比值为