题目内容
14.(1)等差数列{an}中,a7=4,a19=2a9,求数列{an}的通项公式.(2)判断an=n2-n(n∈N*)是否为等差数列.
分析 (1)由a7=4,a19=2a9,结合等差数列的通项公式可求a1,d,进而可求an
(2)根据等差数列的定义进行判断即可.
解答 解:(1)设等差数列{an}的公差为d
∵a7=4,a19=2a9,
∴$\left\{\begin{array}{l}{{a}_{1}+6d=4}\\{{a}_{1}+18d=2({a}_{1}+8d)}\end{array}\right.$,即$\left\{\begin{array}{l}{{a}_{1}+6d=4}\\{{a}_{1}=2d}\end{array}\right.$,
解得,a1=1,d=$\frac{1}{2}$
∴${a}_{n}=1+\frac{1}{2}(n-1)$=$\frac{1+n}{2}$.
(2)当n≥2时,an-an-1=n2-n-[(n-1)2-(n-1)]=2n-2b不是常数,
则an=n2-n(n∈N*)不是等差数列.
点评 本题主要考查了等差数列的通项公式以及等差数列的判断,利用等差数列的定义是解决本题的关键.比较基础.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
5.已知f(x)=ax+btanx+3,且f(-3)=7,则f(3)=( )
| A. | 4 | B. | -1 | C. | -7 | D. | 9 |
6.如果α是第二象限的角,下列各式中成立的是( )
| A. | tanα=-$\frac{sinα}{cosα}$ | B. | cosα=-$\sqrt{1-si{n}^{2}α}$ | C. | sinα=-$\sqrt{1-co{s}^{2}α}$ | D. | tanα=$\frac{cosα}{sinα}$ |
3.若函数f(x)=sin2xcosφ+cos2xsinφ(0<φ<$\frac{π}{2}$),且f(x)≤f($\frac{2π}{9}$),则φ的值为( )
| A. | $\frac{2π}{9}$ | B. | $\frac{π}{9}$ | C. | $\frac{π}{18}$ | D. | $\frac{π}{36}$ |
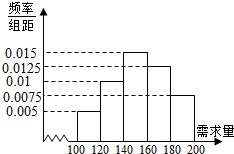 大学生小李毕业后自主创业,买了一辆小型卡车,运输农产品.在输葡萄收获季节,运输1车葡萄.当天批发完获利润500元,当天未批发或有剩余,一律按每车亏损300元计算.根据以往市场调查,得到葡萄收获季节市场需求量的直方图,如图所示,今年葡萄收获的季节,小季给当地农民定了160车葡萄,以X(单位:车,100≤X≤200)表示今年葡萄收获季节的市场需求量,Y(单位:元)表示今年葡萄销售的利润.
大学生小李毕业后自主创业,买了一辆小型卡车,运输农产品.在输葡萄收获季节,运输1车葡萄.当天批发完获利润500元,当天未批发或有剩余,一律按每车亏损300元计算.根据以往市场调查,得到葡萄收获季节市场需求量的直方图,如图所示,今年葡萄收获的季节,小季给当地农民定了160车葡萄,以X(单位:车,100≤X≤200)表示今年葡萄收获季节的市场需求量,Y(单位:元)表示今年葡萄销售的利润.