题目内容
19.已知|$\overrightarrow{p}$|=2$\sqrt{2}$,|$\overrightarrow{q}$|=3,且$\overrightarrow{p}$与$\overrightarrow{q}$的夹角为45°,设$\overrightarrow{a}$=5$\overrightarrow{p}$+2$\overrightarrow{q}$,$\overrightarrow{b}$=$\overrightarrow{p}$-3$\overrightarrow{q}$,求|$\overrightarrow{a}$+$\overrightarrow{b}$|的值.分析 运用向量的数量积的定义,可得$\overrightarrow{p}$•$\overrightarrow{q}$=6,再由向量的平方即为模的平方,化简计算即可得到所求值.
解答 解:|$\overrightarrow{p}$|=2$\sqrt{2}$,|$\overrightarrow{q}$|=3,且$\overrightarrow{p}$与$\overrightarrow{q}$的夹角为45°,
可得$\overrightarrow{p}$•$\overrightarrow{q}$=|$\overrightarrow{p}$|•|$\overrightarrow{q}$|•cos45°=2$\sqrt{2}$×3×$\frac{\sqrt{2}}{2}$=6,
由$\overrightarrow{a}$=5$\overrightarrow{p}$+2$\overrightarrow{q}$,$\overrightarrow{b}$=$\overrightarrow{p}$-3$\overrightarrow{q}$,
可得|$\overrightarrow{a}$+$\overrightarrow{b}$|=|6$\overrightarrow{p}$-$\overrightarrow{q}$|=$\sqrt{36{\overrightarrow{p}}^{2}-12\overrightarrow{p}•\overrightarrow{q}+{\overrightarrow{q}}^{2}}$
=$\sqrt{36×8-12×6+9}$=15.
点评 本题考查向量的数量积的定义和性质,考查向量的平方即为模的平方,考查运算能力,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
4.已知α,β∈(0,$\frac{π}{2}$),且cosα=$\frac{4}{5}$,cos(α+β)=-$\frac{4}{5}$,则cosβ等于( )
| A. | $\frac{4}{25}$ | B. | $-\frac{4}{25}$ | C. | $\frac{7}{25}$ | D. | $-\frac{7}{25}$ |
8.记a=sin(cos2016°),b=sin(sin2016°),c=cos(sin2016°),d=cos(cos2016°),则( )
| A. | d>c>b>a | B. | d>c>a>b | C. | c>d>b>a | D. | a>b>d>c |
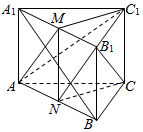 如图,正三棱柱ABC-A1B1C1的底面边长为2,AC1⊥A1B,M是A1B1的中点,N是AB中点,求证:
如图,正三棱柱ABC-A1B1C1的底面边长为2,AC1⊥A1B,M是A1B1的中点,N是AB中点,求证: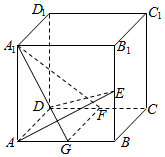 如图在正方体ABCD-A1B1C1D1中,E为BB1的中点,F为CD的中点,G为AB的中点.求证:平面AED⊥平面A1FG.
如图在正方体ABCD-A1B1C1D1中,E为BB1的中点,F为CD的中点,G为AB的中点.求证:平面AED⊥平面A1FG.