题目内容
7.三个人玩传球游戏,每个人都等可能地传给另两人(不自传),若从A发球算起,经4次传球又回到A手中的概率是$\frac{3}{8}$.分析 记三个人为A、B、C,经4次传球的所有可能可用树状图方式列出,由此根据古典概型概率公式能求出结果.
解答  解:记三个人为A、B、C,
解:记三个人为A、B、C,
则经4次传球的所有可能可用树状图方式列出,如右图
每一个分支为一种传球方案,
则基本事件的总数为16,而又回到A手中的事件个数为6个,
根据古典概型概率公式得P=$\frac{6}{16}$=$\frac{3}{8}$.
故答案为:$\frac{3}{8}$.
点评 本题考查概率的求法,是基础题,解题时要认真审题,注意树状图的合理运用.

练习册系列答案
相关题目
15.已知函数f(x)=x|x-2|,x∈R,若方程f(x)=a-|x-1|恰有5个互异的实数根,则实数a的取值范围是( )
| A. | (1,$\frac{5}{4}$) | B. | ($\frac{5}{4}$,+∞) | C. | (1,+∞) | D. | (-∞,$\frac{5}{4}$) |
12.运行如图的程序框图,若输出的y值随着输入的x的增大而增大,则a的取值不可能是( )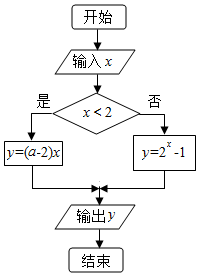

| A. | $\frac{5}{2}$ | B. | $\frac{7}{2}$ | C. | 3 | D. | 4 |
19.已知命题:“若abc=0,则实数a,b,c中至少有一个为0”,用反证法证明该命题时的假设为( )
| A. | 假设a,b,c都不为0 | B. | 假设a,b,c中至少有两个为0 | ||
| C. | 假设a,b,c中至多有两个为0 | D. | 假设a,b,c中至多有一个为0 |
16.若关于x的方程3x=$\frac{a+3}{5-a}$无负数根,则a的取值范围为( )
| A. | a≥1 | B. | a<5 | C. | (-∞,1]∪(5,+∞) | D. | [1,5) |
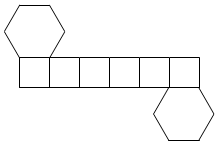 已知一个凸多边形的平面展开图由两个正六边形和六个正方形构成,如图所示,若该凸多面体所有棱长均为1,则其体积V=$\frac{3\sqrt{3}}{2}$.
已知一个凸多边形的平面展开图由两个正六边形和六个正方形构成,如图所示,若该凸多面体所有棱长均为1,则其体积V=$\frac{3\sqrt{3}}{2}$. 如图所示的几何体是由正四棱锥和圆柱组合而成,且该几何体内接于球(正四棱锥的顶点都在球面上),正四棱锥底面边长为2,体积为$\frac{4}{3}$,则圆柱的体积为2π.
如图所示的几何体是由正四棱锥和圆柱组合而成,且该几何体内接于球(正四棱锥的顶点都在球面上),正四棱锥底面边长为2,体积为$\frac{4}{3}$,则圆柱的体积为2π.