题目内容
19．设{an}为等差数列，Sn表示前n项之和，其中a1+a2=0，且S3=3，求该数列的通项公式．分析 由已知条件利用等差数列的通项公式和前n项和公式列出方程组，求出首项与公差，由此能求出该数列的通项公式．
解答 解：∵{an}为等差数列，Sn表示前n项之和，其中a1+a2=0，且S3=3，
∴$\left\{\begin{array}{l}{{a}_{1}+{a}_{1}+d=0}\\{3{a}_{1}+\frac{3×2}{2}d=3}\end{array}\right.$，
解得a1=-1，d=2，
∴an=-1+（n-1）×2=2n-3．
∴该数列的通项公式an=2n-3．
点评 本题考查数列的通项公式的求法，是基础题，解题时要认真审题，注意等差数列的性质的合理运用．
练习册系列答案
相关题目
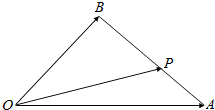如图，在△AOB中，已知P为线段AB上的一点，且$\overrightarrow{BP}$=2$\overrightarrow{PA}$．