题目内容
2．若函数y=ax+cosx是增函数，则实数a的范围是[1，+∞）．分析 求出函数f（x）的导函数，令导函数大于等于0在（-∞，+∞）上恒成立，分析可得a的范围．
解答 解：∵f（x）=ax+cosx，
∴f′（x）=a-sinx，
∵f（x）=ax+cosx在（-∞，+∞）上是单调增函数，
∴a-sinx≥0在（-∞，+∞）上恒成立，
∴a≥1．
故答案为：[1，+∞）．
点评 解决函数的单调性已知求参数范围问题，常求出导函数，令导函数大于等于（或小于等于）0恒成立．
练习册系列答案
相关题目
如图所示的几何体中，四边形ABCD为等腰梯形，AB∥CD，∠DAB=60°，FC⊥平面ABCD，AE⊥BD，CB=CD=CF．
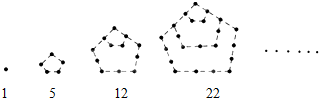如图中的实心点个数1，5，12，22，…，被称为五角形数，其中第1个五角形数记作a1=1，第2个五角形数记作a2=5，第3个五角形数记作a3=12，第4个五角形数记作a4=22，…，若按此规律继续下去，则an=$\frac{{3{n^2}-n}}{2}$．