题目内容
11.设函数y=f(x)(x∈R)的导函数为y=f′(x),且f(x)=f(-x),f′(x)<f(x).则下列三个数:a=ef(2),b=f(3),c=e2f(-1)从小到大排列为b<a<c.(e为自然对数的底数)分析 构造函数g(x)=e-xf(x),利用导数得出其单调性,及利用f(-x)=f(x)即可得出.
解答 解:构造函数g(x)=e-xf(x),
∵f′(x)<f(x),则g′(x)=-e-xf(x)+e-xf′(x)=e-x(f′(x)-f(x))<0.
∴函数g(x)在R上单调递减.
∴e-3f(3)<e-2f(2)<e-1f(1),又f(-1)=f(1),
∴f(3)<ef(2)<e2f(1)=e2f(-1).
故三个数:a=ef(2),b=f(3),c=e2f(-1)从小到大依次排列为:f(3),ef(2),e2f(-1).
故答案为:b<a<c.
点评 本题考查了函数的单调性应用,恰当构造函数g(x)=e-xf(x),熟练掌握利用导数研究函数单调性、奇偶性是解题的关键.

练习册系列答案
相关题目
19.设凸k(k≥3且k∈N)边形的对角线的条数为f(k),则凸k+1边形的对角线的条数为f(k+1)=f(k)+( )
| A. | k-1 | B. | k | C. | k+1 | D. | k2 |
20.已知奇函数f(x)是定义在R上的可导函数,其导函数为f′(x),当x>0时有2f(x)+xf′(x)>x2,则不等式(x+2014)2f(x+2014)+4f(-2)<0的解集为( )
| A. | (-∞,-2012) | B. | (-2016,-2012) | C. | (-∞,-2016) | D. | (-2016,0) |
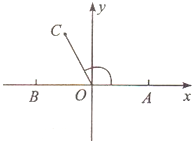 在如图所示的平面直角坐标系中,已知点A(1,0)和点B(-1,0),|$\overrightarrow{OC}$|=1,且∠AOC=x,其中O为坐标原点.
在如图所示的平面直角坐标系中,已知点A(1,0)和点B(-1,0),|$\overrightarrow{OC}$|=1,且∠AOC=x,其中O为坐标原点.