题目内容
在△ABC中,AB=5,AC=3,BC=4,线段MN分别交BC,AB于点M,N,若线段MN分△ABC为面积相等的两部分,求线段MN长度的最小值.
考点:直线的截距式方程
专题:直线与圆
分析:由题意可知△ABC为直角三角形,以CA所在直线为x轴,以CB所在直线为y轴建立平面直角坐标系,设出MN所在直线方程y=kx+b,求出AB所在直线方程,联立求得N的坐标,由△MBN的面积是△ABC面积的一半得到k与b的关系,由两点间的距离公式得到|MN|,转化为含有k的代数式后利用基本不等式求最值.
解答:
解:如图,
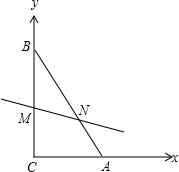
以CA所在直线为x轴,以CB所在直线为y轴建立平面直角坐标系,
由题意可知直线MN的斜率存在,
设其所在直线方程为y=kx+b,
则k>-
,0<b<4,
AB所在直线方程为
+
=1,
联立
,得
,
∴N(
,
),
又|BM|=4-b,
∴S△MNB=
•(4-b)•
=
×3×4,
整理得:b2-8b=6k-8.
|MN|=
=3
=3
≥3
=2.
当且仅当
=
,即k=
时上式等号成立.
∴MN长度的最小值为2.

以CA所在直线为x轴,以CB所在直线为y轴建立平面直角坐标系,
由题意可知直线MN的斜率存在,
设其所在直线方程为y=kx+b,
则k>-
| 4 |
| 3 |
AB所在直线方程为
| x |
| 3 |
| y |
| 4 |
联立
|
|
∴N(
| 12-3b |
| 3k+4 |
| 12k+4b |
| 3k+4 |
又|BM|=4-b,
∴S△MNB=
| 1 |
| 2 |
| 12-3b |
| 3k+4 |
| 1 |
| 4 |
整理得:b2-8b=6k-8.
|MN|=
(
|
=3
| 2 |
|
| 2 |
|
≥3
| 2 |
2×
|
当且仅当
| 3k+4 |
| 9 |
| 25 |
| 9(3k+4) |
| 1 |
| 3 |
∴MN长度的最小值为2.
点评:本题考查了直线的截距式方程,考查了利用基本不等式求最值,考查了学生的灵活变换能力和计算能力,是中档题.

练习册系列答案
相关题目

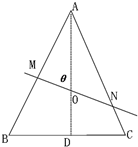 如图,等边△ABC中,AB=3,O为中心,过O的直线交AB于M,交AC于N,设∠AOM=θ(0≤θ≤120°),当θ分别为何值时,
如图,等边△ABC中,AB=3,O为中心,过O的直线交AB于M,交AC于N,设∠AOM=θ(0≤θ≤120°),当θ分别为何值时,