题目内容
已知函数f(x)=
是R上的奇函数
(1)求a的值;
(2)用定义证明该函数在[1,+∞)上的单调性,并求当x∈[2,5]的最大值和最小值.
| x+a |
| x2+1 |
(1)求a的值;
(2)用定义证明该函数在[1,+∞)上的单调性,并求当x∈[2,5]的最大值和最小值.
考点:函数奇偶性的性质
专题:函数的性质及应用
分析:(1)利用函数是奇函数,由f(0)=0即可得到a的值.
(2)利用函数单调性的定义进行判断即可得到结论.
(2)利用函数单调性的定义进行判断即可得到结论.
解答:
解:(1)∵f(x)=
是R上的奇函数,
∴f(0)=0,
即a=0,
此时f(x)=
是奇函数.
(2)设x1,x2,是[1,+∞)上的任意两个数,且1≤x1<x2,
则f(x1)-f(x2)=
-
=
,
∵1≤x1<x2,
∴x2-x1>0,x1x2-1>0,
即f(x1)-f(x2)=
>0,
即f(x1)-f(x2)>0,
f(x1)>f(x2),即函数是减函数.
∴当x∈[2,5]时,函数的最大值为f(2)=
=
,
函数的最小值为f(5)=
=
.
| x+a |
| x2+1 |
∴f(0)=0,
即a=0,
此时f(x)=
| x |
| x2+1 |
(2)设x1,x2,是[1,+∞)上的任意两个数,且1≤x1<x2,
则f(x1)-f(x2)=
| x1 | ||
|
| x2 | ||
|
| (x2-x1)(x1x2-1) | ||||
(
|
∵1≤x1<x2,
∴x2-x1>0,x1x2-1>0,
即f(x1)-f(x2)=
| (x2-x1)(x1x2-1) | ||||
(
|
即f(x1)-f(x2)>0,
f(x1)>f(x2),即函数是减函数.
∴当x∈[2,5]时,函数的最大值为f(2)=
| 2 |
| 22+1 |
| 2 |
| 5 |
函数的最小值为f(5)=
| 5 |
| 25+1 |
| 5 |
| 26 |
点评:本题主要考查函数奇偶性和单调性的判断和应用,根据函数奇偶性和单调性的定义和性质是解决本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
如果x>y>0,则
=( )
| xyyx |
| xxyy |
A、(x-y)
| ||
B、(x-y)
| ||
C、(
| ||
D、(
|


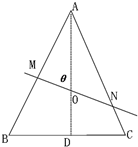 如图,等边△ABC中,AB=3,O为中心,过O的直线交AB于M,交AC于N,设∠AOM=θ(0≤θ≤120°),当θ分别为何值时,
如图,等边△ABC中,AB=3,O为中心,过O的直线交AB于M,交AC于N,设∠AOM=θ(0≤θ≤120°),当θ分别为何值时,