题目内容
如图，P是圆O外一点，过P引圆O的两条割线PAB、PCD，PA=AB=| 5 |
考点：与圆有关的比例线段
专题：选作题,立体几何
分析：根据圆的两条割线，根据割线定理写出关系式，根据所给的三条线段的长度，得到要用的线段的长度，代入关系式，得到关于PC的一元二次方程，解方程得到结果，舍去不合题意的结果．
解答：
解：∵过P引圆O的两条割线PAB、PCD，
∴PA•PB=PC•PD，
∵PA=AB=
，CD=3，
∴
•2
=PC•（PC+3）
∴PC2+3PC-10=0，
∴（PC-2）（PC+5）=0
∴PC=2或PC=-5（舍去）
故答案为：2．
解：∵过P引圆O的两条割线PAB、PCD，∴PA•PB=PC•PD，
∵PA=AB=
| 5 |
∴
| 5 |
| 5 |
∴PC2+3PC-10=0，
∴（PC-2）（PC+5）=0
∴PC=2或PC=-5（舍去）
故答案为：2．
点评：本题考查圆的切割线定理，考查一元二次方程的解法，是一个简单的题目．
练习册系列答案
相关题目
在复平面内与复数z=
所对应的点关于实轴对称的点为A，则A对应的复数为（ ）
| 2i |
| 1+i |
| A、1+i | B、1-i |
| C、-1-i | D、-1+i |
已知a∈R，则“a=-1”是“a2-1+（a-1）i为纯虚数”的（ ）
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
如图，某广场中间有一块扇形绿地OAB，其中O为扇形OAB所在圆的圆心，∠AOB=60°，扇形绿地OAB的半径为r．广场管理部门欲在绿地上修建观光小路：在
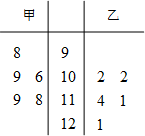在数学趣味知识培训活动中，甲、乙两名学生的5次培训成绩如茎叶图所示：