题目内容
设函数f(x)=xm+ax的导数f'(x)=2x+3,则数列{ }(n∈N*)的前n项和是
}(n∈N*)的前n项和是
- A.

- B.

- C.
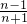
- D.

B
分析:由f(x)=xm+ax的导数f'(x)=mxm-1+a=2x+3,先求出f(x)=x2+3x,设an= =
= ,由此能求出数列{
,由此能求出数列{ }(n∈N*)的前n项和.
}(n∈N*)的前n项和.
解答:∵f(x)=xm+ax的导数f'(x)=mxm-1+a=2x+3,
∴m=2,a=3,
∴f(x)=x2+3x,
设an= ,
,
∴则an= =
= ,
,
∴数列{ }(n∈N*)的前n项和
}(n∈N*)的前n项和
Sn=a1+a2+…+an
=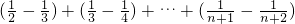
=
= .
.
故选B.
点评:本题考查数列的性质和应用,是基础题.解题时要认真审题,注意导数的性质和应用.
分析:由f(x)=xm+ax的导数f'(x)=mxm-1+a=2x+3,先求出f(x)=x2+3x,设an=
 =
= ,由此能求出数列{
,由此能求出数列{ }(n∈N*)的前n项和.
}(n∈N*)的前n项和.解答:∵f(x)=xm+ax的导数f'(x)=mxm-1+a=2x+3,
∴m=2,a=3,
∴f(x)=x2+3x,
设an=
 ,
,∴则an=
 =
= ,
,∴数列{
 }(n∈N*)的前n项和
}(n∈N*)的前n项和Sn=a1+a2+…+an
=
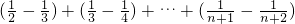
=

=
 .
.故选B.
点评:本题考查数列的性质和应用,是基础题.解题时要认真审题,注意导数的性质和应用.

练习册系列答案
相关题目
设函数f(x)=xm+ax的导函数f′(x)=2x+1,则
f(-x)dx的值等于( )
| ∫ | 2 1 |
A、
| ||
B、
| ||
C、
| ||
D、
|
设函数f(x)=xm+ax的导函数f′(x)=2x+1,则数列{
}(n∈N*)的前n项和是( )
| 1 |
| f(n) |
A、
| ||
B、
| ||
C、
| ||
D、
|