题目内容
4．已知集合A={x|1≤2x≤4}，B={x|（x-a）（x-1）≤0}．（I）求A；
（II）若A∩B=B，求实数a的取值范围．
分析 （I）解不等式1≤2x≤4得出A；
（II）求出B，令B⊆A即可．
解答 解：（I）解不等式1≤2x≤4得0≤x≤2，
∴A={x|0≤x≤2}．
（II）解不等式（x-a）（x-1）≤0得a≤x≤1（a＜1）或1≤x≤a（a＞1）或x=1（a=1），
∵A∩B=B，∴B⊆A，
∴0≤a≤2．
点评 本题考查了集合的关系，不等式的解法，属于基础题．
练习册系列答案
相关题目
7．
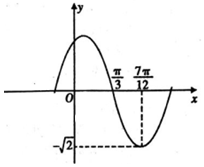函数f（x）=Asin（ωx+φ），（A，ω，φ是常数，A＞0，ω＞0，|φ|≤$\frac{π}{2}$）的部分图象如图所示，若方程f（x）=a在x∈[-$\frac{π}{4}$，$\frac{π}{2}$]上有两个不相等的实数根，则a的取值范围是（ ）
函数f（x）=Asin（ωx+φ），（A，ω，φ是常数，A＞0，ω＞0，|φ|≤$\frac{π}{2}$）的部分图象如图所示，若方程f（x）=a在x∈[-$\frac{π}{4}$，$\frac{π}{2}$]上有两个不相等的实数根，则a的取值范围是（ ）| A． | [$\frac{\sqrt{2}}{2}$，$\sqrt{2}$） | B． | [-$\frac{\sqrt{2}}{2}$，$\sqrt{2}$） | C． | [-$\frac{\sqrt{6}}{2}$，$\sqrt{2}$） | D． | [$\frac{\sqrt{6}}{2}$，$\sqrt{2}$） |
5．给出下列两个命题：命题p：若在边长为1的正方形ABCD内任取一点M，则|MA|≤1的概率为$\frac{π}{4}$．命题q：若函数f（x）=x+$\frac{4}{x}$，（x∈[1，2）），则f（x）的最小值为4．则下列命题为真命题的是（ ）
| A． | p∧q | B． | ￢p | C． | p∧（￢q） | D． | （￢p）∧（￢q） |
12．给出下列两个命题：命题p：若在边长为1的正方形ABCD内任取一点M，则|MA|≤1的概率为$\frac{π}{4}$．命题q：若函数f（x）=x+$\frac{4}{x}，（{x∈[{1，2}]}）$，则f（x）的最小值为4．则下列命题为真命题的是（ ）
| A． | p∧q | B． | ￢p | C． | p∧（￢q） | D． | （￢p）∧（￢q） |