题目内容
14.椭圆$\frac{x^2}{12}+\frac{y^2}{3}=1$的焦点分别为F1和F2,点P在椭圆上,若|PF1|=2,则|PF2|=$4\sqrt{3}-2$.分析 直接利用椭圆的定义与性质,写出结果即可.
解答 解:椭圆$\frac{x^2}{12}+\frac{y^2}{3}=1$的焦点分别为F1和F2,a=2$\sqrt{3}$,
点P在椭圆上,若|PF1|+|PF2|=4$\sqrt{3}$,
|PF1|=2,则|PF2|=4$\sqrt{3}$-2.
故答案为:$4\sqrt{3}-2$
点评 本题考查椭圆的简单性质以及椭圆的定义的应用,是基础题.

练习册系列答案
 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案
相关题目
5.已知集合$M=\{x|x=m+\frac{1}{6},m∈N\}$,$N=\{x|x=\frac{n}{2}-\frac{1}{3},n∈N\}$,则M,N的关系为( )
| A. | M=N | B. | N?M | C. | M?N | D. | N⊆M |
9.直线xcosθ+y-1=0(θ∈R)的倾斜角的取值范围是( )
| A. | [0,π) | B. | [$\frac{π}{4}$,$\frac{3π}{4}$] | C. | [-$\frac{π}{4}$,$\frac{π}{4}$] | D. | [0,$\frac{π}{4}$]∪[$\frac{3π}{4}$,π) |
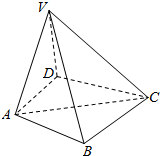 如图,四棱锥V-ABCD中,∠BCD=∠BAD=90°,又∠BCV=∠BAV=90°求证:平面VDB⊥平面ABCD.
如图,四棱锥V-ABCD中,∠BCD=∠BAD=90°,又∠BCV=∠BAV=90°求证:平面VDB⊥平面ABCD.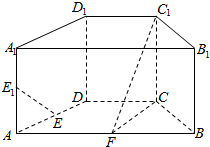 如图,在直四棱柱ABCD-A1B1C1D1中,底面ABCD为等腰梯形,AB∥CD,AB=4,BC=CD=2,AA1=2,E、E1、F分别是棱AD、AA1、AB的中点.
如图,在直四棱柱ABCD-A1B1C1D1中,底面ABCD为等腰梯形,AB∥CD,AB=4,BC=CD=2,AA1=2,E、E1、F分别是棱AD、AA1、AB的中点.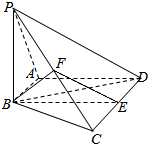 如图,在四棱锥P-ABCD中,AB⊥PA,AB∥CD,且PB=BC=BD=$\sqrt{6}$,CD=2AB=2$\sqrt{2}$,∠PAD=120°,E和F分别是棱CD和PC的中点.
如图,在四棱锥P-ABCD中,AB⊥PA,AB∥CD,且PB=BC=BD=$\sqrt{6}$,CD=2AB=2$\sqrt{2}$,∠PAD=120°,E和F分别是棱CD和PC的中点.