题目内容
9.直线xcosθ+y-1=0(θ∈R)的倾斜角的取值范围是( )| A. | [0,π) | B. | [$\frac{π}{4}$,$\frac{3π}{4}$] | C. | [-$\frac{π}{4}$,$\frac{π}{4}$] | D. | [0,$\frac{π}{4}$]∪[$\frac{3π}{4}$,π) |
分析 先根据直线的方程求出斜率,再求出斜率的取值范围,再根据倾斜角的范围进一步确定倾斜角的范围.
解答 解:直线xcos θ+y-1=0 (θ∈R)的斜率为 k=-cosθ,
∴-1≤k≤1,又直线的倾斜角的范围是[0,π),
故倾斜角α满足0≤α≤$\frac{π}{4}$或$\frac{3π}{4}$≤α<π.
故倾斜角的范围是[0,$\frac{π}{4}$]∪[$\frac{3π}{4}$,π).
故选D.
点评 本题考查直线的倾斜角和斜率的关系,以及倾斜角的取值范围.

练习册系列答案
相关题目
17.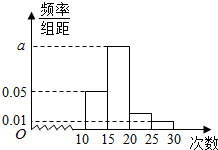 某校对高一年级学生暑假参加社区服务的次数进行了统计,随机抽取了M名学生作为样本,得到这M名学生参加社区服务的次数,根据此数据作出了频率分布统计表和频率分布直方图如下:
某校对高一年级学生暑假参加社区服务的次数进行了统计,随机抽取了M名学生作为样本,得到这M名学生参加社区服务的次数,根据此数据作出了频率分布统计表和频率分布直方图如下:
(1)求表中n,p的值和频率分布直方图中a的值,并估计该校高一学生参加社区服务超过20次的概率;
(2)试估计该校高一学生暑假参加社区服务次数的中位数.
 某校对高一年级学生暑假参加社区服务的次数进行了统计,随机抽取了M名学生作为样本,得到这M名学生参加社区服务的次数,根据此数据作出了频率分布统计表和频率分布直方图如下:
某校对高一年级学生暑假参加社区服务的次数进行了统计,随机抽取了M名学生作为样本,得到这M名学生参加社区服务的次数,根据此数据作出了频率分布统计表和频率分布直方图如下:| 分组 | 频数 | 频率 |
| [10,15) | 10 | 0.25 |
| [15,20) | 25 | n |
| [20,25) | m | p |
| [25,30) | 2 | 0.05 |
| 合计 | M | N |
(2)试估计该校高一学生暑假参加社区服务次数的中位数.
