题目内容
6．已知函数f（x）=alnx+blgx+2，且$f（{\frac{1}{2009}}）=4$，则f（2009）的值为0．分析 直接利用函数的奇偶性的性质化简求解即可．
解答 解：函数y=alnx+blgx是奇函数，
所以函数f（x）=alnx+blgx+2，且$f（{\frac{1}{2009}}）=4$，
可得aln$\frac{1}{2009}$+$blg\frac{1}{2009}$+2=4，
f（2009）=-（aln$\frac{1}{2009}$+$blg\frac{1}{2009}$）+2=-2+2=0．
故答案为：0．
点评 本题考查函数的奇偶性的性质的应用，考查计算能力．
练习册系列答案
相关题目
17．
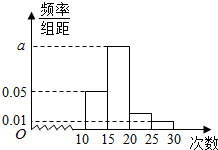某校对高一年级学生暑假参加社区服务的次数进行了统计，随机抽取了M名学生作为样本，得到这M名学生参加社区服务的次数，根据此数据作出了频率分布统计表和频率分布直方图如下：
（1）求表中n，p的值和频率分布直方图中a的值，并估计该校高一学生参加社区服务超过20次的概率；
（2）试估计该校高一学生暑假参加社区服务次数的中位数．
某校对高一年级学生暑假参加社区服务的次数进行了统计，随机抽取了M名学生作为样本，得到这M名学生参加社区服务的次数，根据此数据作出了频率分布统计表和频率分布直方图如下：| 分组 | 频数 | 频率 |
| [10，15） | 10 | 0.25 |
| [15，20） | 25 | n |
| [20，25） | m | p |
| [25，30） | 2 | 0.05 |
| 合计 | M | N |
（2）试估计该校高一学生暑假参加社区服务次数的中位数．
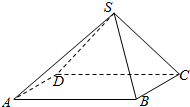如图所示，在四棱锥S-ABCD中，底面ABCD是矩形，侧面SDC⊥底面ABCD，求证：平面SCD⊥平面SBC．