题目内容
已知数列{an}满足a1=x,a2=3x,Sn+1+Sn+Sn-1=3n2+2(n≥2,n∈N*),Sn是数列{an}的前n项和.
(1)若数列{an}为等差数列.
(ⅰ)求数列的通项an;
(ⅱ)若数列{bn}满足bn=2an,数列{cn}满足cn=t2bn+2-tbn+1-bn,试比较数列{bn}前n项和Bn与{cn}前n项和Cn的大小;
(2)若对任意n∈N*,an<an+1恒成立,求实数x的取值范围.
(1)若数列{an}为等差数列.
(ⅰ)求数列的通项an;
(ⅱ)若数列{bn}满足bn=2an,数列{cn}满足cn=t2bn+2-tbn+1-bn,试比较数列{bn}前n项和Bn与{cn}前n项和Cn的大小;
(2)若对任意n∈N*,an<an+1恒成立,求实数x的取值范围.
考点:数列与不等式的综合
专题:等差数列与等比数列,不等式的解法及应用
分析:(1)(ⅰ)由已知可得,an+1+an+an-1=3n2+2-(3n2-6n+5)=6n-3.再结合等差中项的性质即可求出数列的通项公式an;
(ⅱ)根据(ⅰ)可知bn=2an=22n-1,cn=t2bn+2-tbn+1-bn=(16t2-4t-1)bn.从而Bn=b1+b2+…+bn,Cn=c1+c2+…+cn=(16t2-4t-1)(b1+b2+…+bn).只需比较16t2-4t-1与1的大小即可得出Bn与Cn的大小关系;
(2)利用已知条件得出an+3-an=6(n≥2,n∈N*).然后分n=3k-1,n=3k,n=3k+1三种情况讨论,列出不等式组解答即可.
(ⅱ)根据(ⅰ)可知bn=2an=22n-1,cn=t2bn+2-tbn+1-bn=(16t2-4t-1)bn.从而Bn=b1+b2+…+bn,Cn=c1+c2+…+cn=(16t2-4t-1)(b1+b2+…+bn).只需比较16t2-4t-1与1的大小即可得出Bn与Cn的大小关系;
(2)利用已知条件得出an+3-an=6(n≥2,n∈N*).然后分n=3k-1,n=3k,n=3k+1三种情况讨论,列出不等式组解答即可.
解答:
解:(1)(ⅰ)∵Sn+1+Sn+Sn-1=3n2+2(n≥2,n∈N*),①
∴Sn+Sn-1+Sn-2=3(n-1)2+2=3n2-6n+5(n≥3,n∈N*).②
①-②,得
an+1+an+an-1=3n2+2-(3n2-6n+5)=6n-3.
∵数列{an}为等差数列,
∴an+1+an-1=2an.
∴3an=6n-3.
∴an=2n-1(n≥3)③
当n=1时,
a1=1,a2=3符合③式.
∴数列{an}的通项公式为an=2n-1.
(ⅱ)∵an=2n-1.
∴bn=2an=22n-1,
∴cn=t2bn+2-tbn+1-bn
=(16t2-4t-1)bn.
∴Bn=b1+b2+…+bn,
Cn=c1+c2+…+cn
=(16t2-4t-1)(b1+b2+…+bn).
当16t2-4t-1=1,即t=
或t=-
时,Bn=Cn.
当16t2-4t-1>1,即t>
或t<-
时,Bn<Cn.
当16t2-4t-1<1,即-
<t<
时,Bn>Cn.
(2)∵Sn+1+Sn+Sn-1=3n2+2(n≥2,n∈N*),④
∴Sn+2+Sn+1+Sn=3(n+1)2+2(n∈N*)⑤
④-⑤,得
an+2+an+1+an=6n+3(n≥2,n∈N*).⑥
∴an+3+an+2+an+1=6(n+1)+3(n∈N*)⑦
⑥-⑦,得
an+3-an=6(n≥2,n∈N*).
∴当n=1时,an=a1=x.
当n=3k-1时,
an=a3k-1=a2+(k-1)×6
=3x+6k-6
=2n+3x-4.
当n=3k时,
an=a3k=a3+(k-1)×6
=14-9x+6k-6
=2n-9x+8.
当n=3k+1时,
an=a3k+1=a4+(k-1)×6
=1+6x+6k-6
=2n+6x-7,
∵对任意n∈N*,an<an+1恒成立,
∴a1<a2且a3k-1<a3k<a3k+1<a3k+2.
∴
解得,
<x<
.
∴实数x的取值范围为(
,
).
∴Sn+Sn-1+Sn-2=3(n-1)2+2=3n2-6n+5(n≥3,n∈N*).②
①-②,得
an+1+an+an-1=3n2+2-(3n2-6n+5)=6n-3.
∵数列{an}为等差数列,
∴an+1+an-1=2an.
∴3an=6n-3.
∴an=2n-1(n≥3)③
当n=1时,
a1=1,a2=3符合③式.
∴数列{an}的通项公式为an=2n-1.
(ⅱ)∵an=2n-1.
∴bn=2an=22n-1,
∴cn=t2bn+2-tbn+1-bn
=(16t2-4t-1)bn.
∴Bn=b1+b2+…+bn,
Cn=c1+c2+…+cn
=(16t2-4t-1)(b1+b2+…+bn).
当16t2-4t-1=1,即t=
| 1 |
| 2 |
| 1 |
| 4 |
当16t2-4t-1>1,即t>
| 1 |
| 2 |
| 1 |
| 4 |
当16t2-4t-1<1,即-
| 1 |
| 4 |
| 1 |
| 2 |
(2)∵Sn+1+Sn+Sn-1=3n2+2(n≥2,n∈N*),④
∴Sn+2+Sn+1+Sn=3(n+1)2+2(n∈N*)⑤
④-⑤,得
an+2+an+1+an=6n+3(n≥2,n∈N*).⑥
∴an+3+an+2+an+1=6(n+1)+3(n∈N*)⑦
⑥-⑦,得
an+3-an=6(n≥2,n∈N*).
∴当n=1时,an=a1=x.
当n=3k-1时,
an=a3k-1=a2+(k-1)×6
=3x+6k-6
=2n+3x-4.
当n=3k时,
an=a3k=a3+(k-1)×6
=14-9x+6k-6
=2n-9x+8.
当n=3k+1时,
an=a3k+1=a4+(k-1)×6
=1+6x+6k-6
=2n+6x-7,
∵对任意n∈N*,an<an+1恒成立,
∴a1<a2且a3k-1<a3k<a3k+1<a3k+2.
∴
|
解得,
| 13 |
| 15 |
| 7 |
| 6 |
∴实数x的取值范围为(
| 13 |
| 15 |
| 7 |
| 6 |
点评:本题考查等差数列,等比数列的性质,数列与不等式的综合问题的解答等知识,属于难题.

练习册系列答案
相关题目
复数z=
在复平面上对应的点的坐标为( )
| 1-i |
| 2+i |
A、(
| ||||
B、(
| ||||
C、(
| ||||
D、(
|
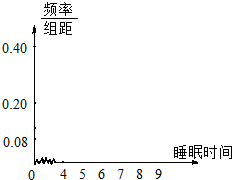 某学校为了了解学生的日平均睡眠时间(单位:h),随机选择了n名同学进行调查.下表是这n名同学的日睡眠时间的频率分布表.
某学校为了了解学生的日平均睡眠时间(单位:h),随机选择了n名同学进行调查.下表是这n名同学的日睡眠时间的频率分布表.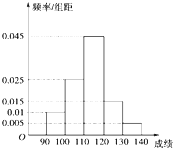 某校高三数学竞赛初赛考试后,对90分以上(含90分)的成绩进行统计,其频率分布直方图如图所示.若130~140分数段的人数为2人.
某校高三数学竞赛初赛考试后,对90分以上(含90分)的成绩进行统计,其频率分布直方图如图所示.若130~140分数段的人数为2人. 如图,⊙O中,直径AB和弦DE互相垂直,C是DE延长线上一点,连结BC与圆O交于F,若∠DBC=
如图,⊙O中,直径AB和弦DE互相垂直,C是DE延长线上一点,连结BC与圆O交于F,若∠DBC=