题目内容
已知数列{an}中,a1=5,an=2an-1+2n-1(n∈N*且n≥2).
(1)求a2、a3的值;
(2)若数列{
}为等差数列,求实数λ的值;
(3)求数列{an}的前n项和Sn.
(1)求a2、a3的值;
(2)若数列{
| an+λ |
| 2n |
(3)求数列{an}的前n项和Sn.
考点:数列的求和,等差关系的确定,数列递推式
专题:等差数列与等比数列
分析:(1)由已知条件,分别令n=2,n=3,由递推思想能求出a2、a3的值.
(2)由已知条件推导出
=
+1-
,由此能求出数列{
}为等差数列时实数λ的值.
(3)由(2)知数列{
}是首项为2,公差为1的等差数列,从而能求出an=(n+1)•2n+1,由此利用裂项求和法能求出数列{an}的前n项和Sn.
(2)由已知条件推导出
| an+λ |
| 2n |
| an-1+λ |
| 2n-1 |
| 1+λ |
| 2n |
| an+λ |
| 2n |
(3)由(2)知数列{
| an-1 |
| 2n |
解答:
解:(1)∵a1=5,an=2an-1+2n-1(n∈N*且n≥2),
∴a2=2×5+22-1=10+4-1=13,
a3=2×13+23-1=26+8-1=33.…(3分)
(2)∵a1=5,an=2an-1+2n-1(n∈N*且n≥2),
∴
=
=
+1-
.…(5分)
∴当且仅当
=0,即λ=-1时,
数列{
}为等差数列.…(7分)
(3)由(2)的结论知:数列{
}是首项为
=2,
公差为1的等差数列,
∴
=2+(n-1)×1=n+1,…(9分)
∴an=(n+1)•2n+1,…(10分)
∴Sn=2×2+3×22+4×23+…+(n+1)•2n+n,
2Sn=2×22+3×23+4×24+…+(n+1)•2n+1+2n,…(11分)
两式相减,得
-Sn=4+(22+23+…+2n)-(n+1)•2n+1-n,…(12分)
∴Sn=n•(2n+1+1),(n∈N*).…(14分)
∴a2=2×5+22-1=10+4-1=13,
a3=2×13+23-1=26+8-1=33.…(3分)
(2)∵a1=5,an=2an-1+2n-1(n∈N*且n≥2),
∴
| an+λ |
| 2n |
| 2an-1+2n-1+λ |
| 2n |
=
| an-1+λ |
| 2n-1 |
| 1+λ |
| 2n |
∴当且仅当
| 1+λ |
| 2n |
数列{
| an+λ |
| 2n |
(3)由(2)的结论知:数列{
| an-1 |
| 2n |
| a1-1 |
| 2 |
公差为1的等差数列,
∴
| an-1 |
| 2n |
∴an=(n+1)•2n+1,…(10分)
∴Sn=2×2+3×22+4×23+…+(n+1)•2n+n,
2Sn=2×22+3×23+4×24+…+(n+1)•2n+1+2n,…(11分)
两式相减,得
-Sn=4+(22+23+…+2n)-(n+1)•2n+1-n,…(12分)
∴Sn=n•(2n+1+1),(n∈N*).…(14分)
点评:本题考查数列中某项值的求法,考查等差数列的性质的应用,考查数列前n项和的求法,解题时要认真审题,注意裂项求和法的合理运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知实数x,y满足方程(x-2)2+y2=1,那么
的最大值为( )
| y |
| x |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
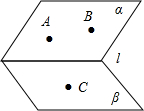 如图,已知平面α∩β=l,点A∈α,点B∈α,点C属于β,且A∉l,B∉l,直线AB与l不平行,那么平面ABC与平面β的交线与l有什么关系?证明你的结论.
如图,已知平面α∩β=l,点A∈α,点B∈α,点C属于β,且A∉l,B∉l,直线AB与l不平行,那么平面ABC与平面β的交线与l有什么关系?证明你的结论. 某校同学设计一个如图所示的“蝴蝶形图案(阴影区域)”,其中AC、BD是过抛物线Γ焦点F的两条弦,且其焦点F(0,1),
某校同学设计一个如图所示的“蝴蝶形图案(阴影区域)”,其中AC、BD是过抛物线Γ焦点F的两条弦,且其焦点F(0,1),