题目内容
7. 如图,在四棱锥P-ABCD中,底面ABCD为矩形,平面PCD⊥平面ABCD,BC=1,AB=2,$PC=PD=\sqrt{2}$,E为PA中点.
如图,在四棱锥P-ABCD中,底面ABCD为矩形,平面PCD⊥平面ABCD,BC=1,AB=2,$PC=PD=\sqrt{2}$,E为PA中点.(Ⅰ)求证:PC∥平面BED;
(Ⅱ)求二面角A-PC-D的余弦值;
(Ⅲ)在棱PC上是否存在点M,使得BM⊥AC?若存在,求$\frac{PM}{PC}$的值;若不存在,说明理由.
分析 (Ⅰ)设AC与BD的交点为F,连结EF,推导出EF∥PC.由此能证明PC∥平面BED.
(Ⅱ)取CD中点O,连结PO.推导出PO⊥CD,取AB中点G,连结OG,建立空间直角坐标系O-xyz,利用向量法能求出二面角A-PC-B的余弦值.
(Ⅲ)设M是棱PC上一点,则存在λ∈[0,1]使得$\overrightarrow{PM}=λ\overrightarrow{PC}$.利用向量法能求出在棱PC上存在点M,使得BM⊥AC.此时,$\frac{PM}{PC}$=$\frac{1}{2}$
解答 (共14分)
证明:(Ⅰ)设AC与BD的交点为F,连结EF.
因为ABCD为矩形,所以F为AC的中点.
在△PAC中,由已知E为PA中点,
所以EF∥PC.
又EF?平面BFD,PC?平面BFD,
所以PC∥平面BED. …(5分)
(Ⅱ)取CD中点O,连结PO.
因为△PCD是等腰三角形,O为CD的中点,
所以PO⊥CD.
又因为平面PCD⊥平面ABCD,
PO?平面PCD,所以PO⊥平面ABCD.
取AB中点G,连结OG,由题设知四边形ABCD为矩形,
所以OF⊥CD.所以PO⊥OG.…(1分)
如图建立空间直角坐标系O-xyz,
则A(1,-1,0),C(0,1,0),P(0,0,1),D(0,-1,0),
B(1,1,0),O(0,0,0),G(1,0,0).
$\overrightarrow{AC}$=(-1,2,0),$\overrightarrow{PC}$=(0,1,-1).
设平面PAC的法向量为$\overrightarrow{n}$=(x,y,z),
则$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{AC}=-x+2y=0}\\{\overrightarrow{n}•\overrightarrow{PC}=y-z=0}\end{array}\right.$,令z=1,得$\overrightarrow{n}$=(2,1,1).
平面PCD的法向量为$\overrightarrow{OG}$=(1,0,0).
设$\overrightarrow{n},\overrightarrow{OG}$的夹角为α,所以cosα=$\frac{|\overrightarrow{n}•\overrightarrow{OG}|}{|\overrightarrow{n}•\overrightarrow{OG}|}$=$\frac{\sqrt{6}}{3}$.
由图可知二面角A-PC-D为锐角,
所以二面角A-PC-B的余弦值为$\frac{\sqrt{6}}{3}$.…(10分)
(Ⅲ)设M是棱PC上一点,则存在λ∈[0,1]使得$\overrightarrow{PM}=λ\overrightarrow{PC}$.
因此点M(0,λ,1-λ),$\overrightarrow{BM}$=(-1,λ-1,1-λ),$\overrightarrow{AC}$=(-1,2,0).
由$\overrightarrow{BM}•\overrightarrow{AC}=0$,得1+2(λ-1)=0,解得$λ=\frac{1}{2}$.
因为$λ=\frac{1}{2}$∈[0,1],所以在棱PC上存在点M,使得BM⊥AC.
此时,$\frac{PM}{PC}$=$\frac{1}{2}$. …(14分)
点评 本题考查线面平行的证明,考查二面角的余弦值的求法,考查线段比值的求法,是中档题,解题时要认真审题,注意向量法的合理运用.

 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案| A. | -1 | B. | 0 | C. | 1 | D. | 2 |
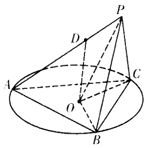 如图所示,正三角形ABC的外接圆半径为2,圆心为O,PB=PC=2,D为AP上一点,AD=2DP,点D在平面ABC内的射影为圆心O.
如图所示,正三角形ABC的外接圆半径为2,圆心为O,PB=PC=2,D为AP上一点,AD=2DP,点D在平面ABC内的射影为圆心O.