题目内容
11.已知$\frac{tanα}{tanα-1}$=-1,则cos2($\frac{π}{2}$+α)-sin(π-α)cos(π+α)+2=$\frac{13}{5}$.分析 求出tanα,进而使用同角三角函数的关系解出sin2α,cos2α,使用诱导公式化简即可得出答案.
解答 解:∵$\frac{tanα}{tanα-1}$=-1,∴tanα=$\frac{1}{2}$.∴sinα=$\frac{1}{2}cosα$.
∵sin2α+cos2α=1,∴sin2α=$\frac{1}{5}$,cos2α=$\frac{4}{5}$.
∴cos2($\frac{π}{2}$+α)-sin(π-α)cos(π+α)+2=sin2α+sinαcosα+2
=sin2α+$\frac{1}{2}$cos2α+2=$\frac{1}{5}+\frac{1}{2}×\frac{4}{5}+2$=$\frac{13}{5}$.
故答案为:$\frac{13}{5}$.
点评 本题考查了使用诱导公式进行化简求值,要熟练掌握公式.

练习册系列答案
相关题目
1.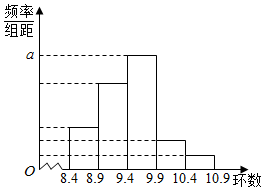 某射击训练基地教练为了对某运动员的成绩做一分析,随机抽取该名运动员的t次射击成绩作为一个样本,根据此数据做出了频数与频率的统计表和频率分布直方图如下:
某射击训练基地教练为了对某运动员的成绩做一分析,随机抽取该名运动员的t次射击成绩作为一个样本,根据此数据做出了频数与频率的统计表和频率分布直方图如下:
(I)求表中t,p及图中a的值;
(Ⅱ)在所取的样本中,从不少于9.9环的成绩中任取3次,X表示所取成绩不少于10.4的次数,求随机变量X的分布列及数学期望.
 某射击训练基地教练为了对某运动员的成绩做一分析,随机抽取该名运动员的t次射击成绩作为一个样本,根据此数据做出了频数与频率的统计表和频率分布直方图如下:
某射击训练基地教练为了对某运动员的成绩做一分析,随机抽取该名运动员的t次射击成绩作为一个样本,根据此数据做出了频数与频率的统计表和频率分布直方图如下:| 分组 | 频数 | 频率 |
| [8.4,8.9) | 9 | 0.15 |
| [8.9,9.4) | m | 0.3 |
| [9.4,9.9) | 24 | n |
| [9.9,10.4) | q | p |
| [10.4,10.9) | 3 | 0.05 |
| 合计 | t | 1 |
(Ⅱ)在所取的样本中,从不少于9.9环的成绩中任取3次,X表示所取成绩不少于10.4的次数,求随机变量X的分布列及数学期望.
6.下列命题:①三角形是一个是平面;②平行四边形是一个平面;③梯形是一个平面图形;④四边相等的四边形是菱形.其中正确的是( )
| A. | ③ | B. | ①② | C. | ①②③ | D. | ①②③④ |
15.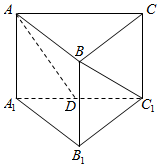 已知在直三棱柱ABC-A1B1C1中,∠ABC=90°,AB=BC=AA1=2,点D是A1C1的中点,则异面直线AD和BC1所成角的大小为( )
已知在直三棱柱ABC-A1B1C1中,∠ABC=90°,AB=BC=AA1=2,点D是A1C1的中点,则异面直线AD和BC1所成角的大小为( )
 已知在直三棱柱ABC-A1B1C1中,∠ABC=90°,AB=BC=AA1=2,点D是A1C1的中点,则异面直线AD和BC1所成角的大小为( )
已知在直三棱柱ABC-A1B1C1中,∠ABC=90°,AB=BC=AA1=2,点D是A1C1的中点,则异面直线AD和BC1所成角的大小为( )| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{π}{4}$ | D. | $\frac{π}{2}$ |
