Question

2．已知抛物线C：y²=2px（p＞0）上的点M的横坐标为2，且|MF|=3，F是抛物线的焦点．
（1）求抛物线C的方程；
（2）过点M（-1，0）的直线l与抛物线C相交于A、B两点．设线段AB的中点为P，记直线FA，FB，FP的斜率分别为k₁，k₂，k₃，求当k₁k₂+k₃+1=0时的直线l的方程．

Answer 1

分析 （1）由抛物线定义结合抛物线的焦半径公式求得p值，则抛物线方程可求；
（2）设出直线l的方程，联立直线方程和抛物线方程，利用根与系数的关系得到A，B的横坐标的和与积，再由k₁k₂+k₃+1=0求得k值，则直线l的方程可求．

解答 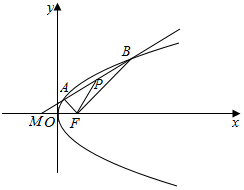解：（1）由已知：2+$\frac{p}{2}$=3，∴P=2，
故抛物线C的方程为：y²=4x；
（2）如图，
设直线l的方程为y=k（x+1），
联立$\left\{\begin{array}{l}{y=kx+k}\\{{y}^{2}=4x}\end{array}\right.$，得k²x²+（2k²-4）x+k²=0．
∴△=（2k²-4）²-4k⁴=16-16k²＞0，即-1＜k＜1．
设A（x₁，y₁），B（x₂，y₂），则P（$\frac{{x}_{1}+{x}_{2}}{2}，\frac{{y}_{1}+{y}_{2}}{2}$），
则${x}_{1}+{x}_{2}=\frac{4-2{k}^{2}}{{k}^{2}}，{x}_{1}{x}_{2}=1$①，
${k}_{1}=\frac{{y}_{1}}{{x}_{1}-1}$，${k}_{2}=\frac{{y}_{2}}{{x}_{2}-1}$，${k}_{3}=\frac{\frac{{y}_{1}+{y}_{2}}{2}}{\frac{{x}_{1}+{x}_{2}}{2}-1}=\frac{{y}_{1}+{y}_{2}}{{x}_{1}+{x}_{2}-2}$
由k₁k₂+k₃+1=0，得
$\frac{{k}^{2}（{x}_{1}+{x}_{2}+{x}_{1}{x}_{2}+1）}{{x}_{1}{x}_{2}-（{x}_{1}+{x}_{2}）+1}$$+\frac{k（{x}_{1}+{x}_{2}）+2k}{{x}_{1}+{x}_{2}-2}+1$=0②，
把①代入②整理得：$\frac{2{k}^{2}-k-1}{{k}^{2}-1}=0$，
解得：k=1（舍）或$k=-\frac{1}{2}$．
∴直线l的方程为y=$-\frac{x}{2}-\frac{1}{2}$，即x+2y+1=0．

点评 本题考查抛物线的简单性质，考查了直线和抛物线的位置关系的应用，体现了整体运算思想方法，是中档题．