题目内容
15.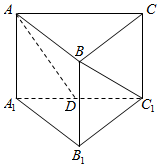 已知在直三棱柱ABC-A1B1C1中,∠ABC=90°,AB=BC=AA1=2,点D是A1C1的中点,则异面直线AD和BC1所成角的大小为( )
已知在直三棱柱ABC-A1B1C1中,∠ABC=90°,AB=BC=AA1=2,点D是A1C1的中点,则异面直线AD和BC1所成角的大小为( )| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{π}{4}$ | D. | $\frac{π}{2}$ |
分析 以B1为原点,B1A1为x轴,B1C1为y轴,B1B为z轴,建立空间直角坐标系,利用向量法能求出异面直线AD和BC1所成角的大小.
解答 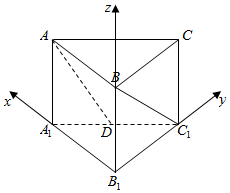 解:以B1为原点,B1A1为x轴,B1C1为y轴,B1B为z轴,建立空间直角坐标系,
解:以B1为原点,B1A1为x轴,B1C1为y轴,B1B为z轴,建立空间直角坐标系,
∵在直三棱柱ABC-A1B1C1中,∠ABC=90°,AB=BC=AA1=2,点D是A1C1的中点,
∴A(2,0,2),D(1,1,0),B(0,0,2),C1(0,2,0),
$\overrightarrow{AD}$=(-1,1,-2),$\overrightarrow{B{C}_{1}}$=(0,2,-2),
设异面直线AD和BC1所成角为α,
则cosα=$\frac{|\overrightarrow{AD}•\overrightarrow{B{C}_{1}}|}{|\overrightarrow{AD}|•|\overrightarrow{B{C}_{1}}|}$=$\frac{|0+2+4|}{\sqrt{6}×\sqrt{8}}$=$\frac{\sqrt{3}}{2}$.
∴异面直线AD和BC1所成角的大小为$\frac{π}{6}$.
故选:A.
点评 本题考查异面直线所成角的求法,是基础题,解题时要认真审题,注意向量法的合理运用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
3.与椭圆$\frac{x^2}{5}+{y^2}=1$有相同的焦点,且一条渐近线方程是$y=\sqrt{3}x$的双曲线方程是( )
| A. | ${y^2}-\frac{x^2}{3}=1$ | B. | $\frac{x^2}{3}-{y^2}=1$ | C. | $\frac{y^2}{3}-{x^2}=1$ | D. | ${x^2}-\frac{y^2}{3}=1$ |
10.已知$a={log_{0.3}}0.2,b={0.2^{0.5}},c=lg0.4$,则a、b、c之间的大小关系为( )
| A. | a>b>c | B. | b>a>c | C. | a>c>b | D. | b>c>a |
20.已知向量$\overrightarrow a$,$\overrightarrow b$的夹角为$\frac{π}{3}$,且$|{\overrightarrow a}|=1$,$|{\overrightarrow a+\overrightarrow b}|=\sqrt{7}$,则$|{\overrightarrow b}|$等于( )
| A. | 2 | B. | 3 | C. | $\sqrt{3}$ | D. | 4 |
7.已知数列{an}满足a1=1,${a_{n+1}}=\left\{{\begin{array}{l}{2{a_n},n为正奇数}\\{{a_n}+1,n为正偶数}\end{array}}\right.$,则254是该数列的( )
| A. | 第14项 | B. | 第12项 | C. | 第10项 | D. | 第8项 |
4.在平面直角坐标系xOy中,已知点F1(-5,0),F2(5,0),动点P满足|PF1|-|PF2|=8,则点P的轨迹是( )
| A. | 椭圆 | B. | 双曲线 | C. | 双曲线的左支 | D. | 双曲线的右支 |
5.从一堆产品(其中正品与次品都多于2件)中任取2件,观察正品件数和次品件数.则下列事件是互斥事件但不是对立事件的是( )
| A. | 恰好有1件次品和恰好有2件次品 | B. | 至少有1件次品和全是次品 | ||
| C. | 至少有1件正品和至少有1件次品 | D. | 至少有1件次品和全是正品 |