题目内容
在平面直角坐标系xOy中,已知定点F(1,0),点P在y轴上运动,点M在x轴上,点N为平面内的动点,且满足
•
=0,
+
=0.
(1)求动点N的轨迹C的方程;
(2)设点Q是直线l:x=-1上任意一点,过点Q作轨迹C的两条切线QS,QT,切点分别为S,T,设切线QS,QT的斜率分别为k1,k2,直线QF的斜率为k0,求证:k1+k2=2k0.
| PM |
| PF |
| PM |
| PN |
(1)求动点N的轨迹C的方程;
(2)设点Q是直线l:x=-1上任意一点,过点Q作轨迹C的两条切线QS,QT,切点分别为S,T,设切线QS,QT的斜率分别为k1,k2,直线QF的斜率为k0,求证:k1+k2=2k0.
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线中的最值与范围问题
分析:(1)设点N(x,y),M(a,0),P(0,b),由已知条件推导出点M(-x,0),P(0,
),由此能求出动点N的轨迹C的方程.
(2)设点Q(-1,t),联立方程
,得k2x2+2(k2+kt-2)x+(k+t)2=0,由此利用根的判别式和韦达定理能证明k1+k2=2k0.
| y |
| 2 |
(2)设点Q(-1,t),联立方程
|
解答:
 (1)解:设点N(x,y),M(a,0),P(0,b).
(1)解:设点N(x,y),M(a,0),P(0,b).
∵
+
=0可知,∴点P是MN的中点,
∴
,即
,
∴点M(-x,0),P(0,
).
∴
=(-x,-
),
=(1,-
). …3分
∵
•
=0,∴-x+
=0,即y2=4x.
∴动点N的轨迹C的方程为y2=4x.…5分
(2)证明:设点Q(-1,t),
由于过点Q的直线y-t=k(x+1)与轨迹C:y2=4x相切,
联立方程
,
整理得k2x2+2(k2+kt-2)x+(k+t)2=0.…7分
则△=4(k2+kt-2)2-4k2(k+t)2=0,
化简得k2+tk-1=0.
由题意知k1,k2是关于k的方程k2+tk-1=0的两个根,
∴k1+k2=-t.
又k0=-
,∴k1+k2=2k0.
∴k1+k2=2k0.…10分.
 (1)解:设点N(x,y),M(a,0),P(0,b).
(1)解:设点N(x,y),M(a,0),P(0,b).∵
| PM |
| PN |
∴
|
|
∴点M(-x,0),P(0,
| y |
| 2 |
∴
| PM |
| y |
| 2 |
| PF |
| y |
| 2 |
∵
| PM |
| PF |
| y2 |
| 4 |
∴动点N的轨迹C的方程为y2=4x.…5分
(2)证明:设点Q(-1,t),
由于过点Q的直线y-t=k(x+1)与轨迹C:y2=4x相切,
联立方程
|
整理得k2x2+2(k2+kt-2)x+(k+t)2=0.…7分
则△=4(k2+kt-2)2-4k2(k+t)2=0,
化简得k2+tk-1=0.
由题意知k1,k2是关于k的方程k2+tk-1=0的两个根,
∴k1+k2=-t.
又k0=-
| t |
| 2 |
∴k1+k2=2k0.…10分.
点评:本题考查点的轨迹方程的求法,考查斜率和相等的证明,解题时要认真审题,注意根的判别式和韦达定理的合理运用.

练习册系列答案
相关题目
若向量
=(1,1),
=(1,-1),
=(-1,2),则
+2
-
=( )
| a |
| b |
| c |
| a |
| b |
| c |
| A、(4,-3) |
| B、(4,-2) |
| C、(1,2) |
| D、(2,-3) |
在(1+x-
)4的展开式中,常数项是( )
| 1 |
| x2 |
| A、1 | B、13 | C、-11 | D、-2 |
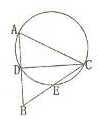 已知,在△ABC中,D是AB上一点,△ACD的外接圆交BC于点E,AB=2BE.
已知,在△ABC中,D是AB上一点,△ACD的外接圆交BC于点E,AB=2BE.