题目内容
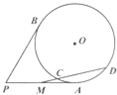如图，P是圆O外一点，PA，PB是圆O的两条切线，切点分别为A，B，PA中点为M，过M作圆O的一条割线交圆O于C，D两点，若PB=2| 3 |
考点：与圆有关的比例线段
专题：立体几何
分析：由切割线定理，得MA2=MC•MD，由此能求出CD．
解答：
解：由已知得MA=
PA=
PB=
，
∵MA是切线，MCD是割线，
∴MA2=MC•MD，
∵MC=1，∴3=1×（1+CD），
解得CD=2．
故答案为：2．
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
∵MA是切线，MCD是割线，
∴MA2=MC•MD，
∵MC=1，∴3=1×（1+CD），
解得CD=2．
故答案为：2．
点评：本题考查与圆有关的线段长的求法，是基础题，解题时要认真审题，注意切割线定理的合理运用．
练习册系列答案
相关题目
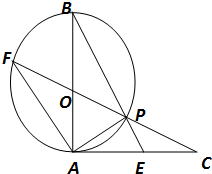已知：如图，AB是⊙O的直径，AC与⊙O相切于点A，且AC=AB，CO与⊙O相交于点P，CO的延长线与⊙O相交于点F，BP的延长线与AC相交于点E．函数y=
的定义域为（ ）
log
|
A、（1，
| ||
B、[1，
| ||
| C、（1，2] | ||
| D、（1，2） |
若函数f（x）=
的定义域为（ ）
|
| A、[0，1） |
| B、（0，1） |
| C、（-∞，0]∪（1，+∞） |
| D、（-∞，0）∪（1，+∞） |
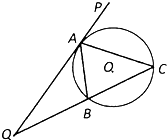如图，直线 PQ与⊙O相切于点 A，A B是⊙O的弦，∠P A B的平分线 AC交⊙O于点C，连结C B，并延长与直线 PQ相交于点Q．
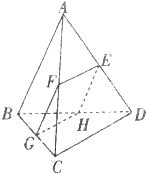如图，在四面体ABCD中，BC-AB，BD-AD截面EFGH平行于对棱AB和CD．