题目内容
已知各项都为整数的等差数列{an}的前n项和为Sn,若S5=35,且a2,a3+1,a6成等比数列.
(1)求{an}的通项公式;
(2)记bn=
的前n项和为Tn,求证Tn<
.
(1)求{an}的通项公式;
(2)记bn=
| an |
| 3n |
| 5 |
| 4 |
考点:数列的求和,数列与不等式的综合
专题:等差数列与等比数列
分析:(1)利用等差数列与等比数列的通项公式即可得出;
(2)利用“错位相减法”与等比数列的前n项和公式可得Tn,即可证明.
(2)利用“错位相减法”与等比数列的前n项和公式可得Tn,即可证明.
解答:
(1)解:设等差数列{an}的公差为d,∵a2,a3+1,a6成等比数列,∴(a3+1)2=a2•a6,
∵S5=35,∴
=5a3=35,解得a3=7.
∴
,又d为整数,
解得
,
∴a1=1+3(n-1)=3n-2.
(2)证明:bn=
=
,
∴Tn=
+
+
+…+
+
,
3Tn=1+
+
+…+
,
∴2Tn=1+
+
+…+
-
=3×
-2-
=
-
,
∴Tn=
-
.
∵S5=35,∴
| 5(a1+a5) |
| 2 |
∴
|
解得
|
∴a1=1+3(n-1)=3n-2.
(2)证明:bn=
| an |
| 3n |
| 3n-2 |
| 3n |
∴Tn=
| 1 |
| 3 |
| 4 |
| 32 |
| 7 |
| 33 |
| 3n-5 |
| 3n-1 |
| 3n-2 |
| 3n |
3Tn=1+
| 4 |
| 3 |
| 7 |
| 32 |
| 3n-2 |
| 3n-1 |
∴2Tn=1+
| 3 |
| 3 |
| 3 |
| 32 |
| 3 |
| 3n-1 |
| 3n-2 |
| 3n |
1-(
| ||
1-
|
| 3n-2 |
| 3n |
| 5 |
| 2 |
| 6n+5 |
| 2•3n |
∴Tn=
| 5 |
| 4 |
| 6n+5 |
| 4×3n |
点评:本题考查了“错位相减法”、等差数列与等比数列的前n项和公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目
若球的半径扩大到原来的2倍,那么体积扩大到原来的( )
| A、64倍 | B、16倍 |
| C、8倍 | D、4倍 |
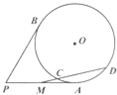 如图,P是圆O外一点,PA,PB是圆O的两条切线,切点分别为A,B,PA中点为M,过M作圆O的一条割线交圆O于C,D两点,若PB=2
如图,P是圆O外一点,PA,PB是圆O的两条切线,切点分别为A,B,PA中点为M,过M作圆O的一条割线交圆O于C,D两点,若PB=2
 已知A,B两点分别在射线CM,CN(不含端点C)上运动,∠MCN=
已知A,B两点分别在射线CM,CN(不含端点C)上运动,∠MCN=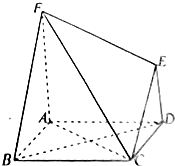 在如图所示的多面体ABCDEF中,四边形ABCD是正方形,AF⊥平面ABCD,DE⊥平面ABCD,且AF=2DE
在如图所示的多面体ABCDEF中,四边形ABCD是正方形,AF⊥平面ABCD,DE⊥平面ABCD,且AF=2DE