题目内容
化简
．
sin(3π-α)cos(α-
| ||||
tan(α-5π)cos(
|
考点：运用诱导公式化简求值
专题：三角函数的求值
分析：原式利用诱导公式化简，计算即可得到结果．
解答：
解：原式=
=cosα．
| sinα•sinα•cosα |
| tanα•(-sinα)(-cosα) |
点评：此题考查了运用诱导公式化简求值，熟练掌握诱导公式是解本题的关键．
练习册系列答案
相关题目
已知函数：
①f（x）=3lnx；
②f（x）=3ecosx；
③f（x）=3ex；
④f（x）=3cosx．
其中对于f（x）定义域内的任意一个自变量x1都存在唯一一个自变量x2，使
=3成立的函数是（ ）
①f（x）=3lnx；
②f（x）=3ecosx；
③f（x）=3ex；
④f（x）=3cosx．
其中对于f（x）定义域内的任意一个自变量x1都存在唯一一个自变量x2，使
| f(x1)f(x2) |
| A、③ | B、②③ | C、①②④ | D、④ |
已知i是虚数单位，且（x-i）（1-i）=y，则实数x，y分别为（ ）
| A、x=-1，y=1 |
| B、x=-1，y=2 |
| C、x=1，y=1 |
| D、x=-1，y=-2 |
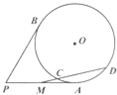如图，P是圆O外一点，PA，PB是圆O的两条切线，切点分别为A，B，PA中点为M，过M作圆O的一条割线交圆O于C，D两点，若PB=2