题目内容

已知sin（θ+
π
4
）=
3
5
，θ为钝角，则sinθ=
 
．
考点：两角和与差的正弦函数
专题：三角函数的求值
分析：根据θ的范围求得cos（θ+
π
4
）的值，进而利用两角和与差的正弦函数求得答案．
解答： 解：∵θ为钝角，
∴
3π
4
＜θ+
π
4
＜
5π
4
，
∴cos（θ+
π
4
）=-
1-
9
25
=-
4
5
，
∴sinθ=sin（θ+
π
4
-
π
4
）=sin（θ+
π
4
）cos
π
4
-cos（θ+
π
4
）sin
π
4
=
3
5
×
2
2
+
4
5
×
2
2
=
7
2
10
，
故答案为：
7
2
10
．
点评：本题主要考查了两角和与差的正弦函数公式的应用．考查了学生对基础公式的记忆．
练习册系列答案
相关题目
已知直线l经过两条直线l1：x+y-4=0和l2：x-y+2=0的交点，直线l3：2x-y-1=0；
（1）若l∥l3，求l的直线方程；
（2）若l⊥l3，求l的直线方程．
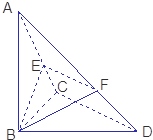已知△BCD中，∠BCD=90°，BC=CD=a，AB⊥平面BCD，∠ADB=60°，E、F分别是AC、AD上的动点，且
AE
AC
=
AF
AD
=λ(0＜λ＜1)．
（Ⅰ）求证：不论λ为何值，总有平面BEF⊥平面ABC；
（Ⅱ）求二面角A-CD-B的正切值；
（Ⅲ）当λ为何值时，平面BEF⊥平面ACD？
一四面体底面为2，2，1的等腰三角形，侧棱都为2，则其体积为
 
．
设集合A=（-∞，a]，B=（b，+∞），a∈N，b∈R，且A∩B∩N={2}，则a+b的取值区间是
 
．
关于函数f(x)=lg
x2+1
2|x|
(x≠0，x∈R)，有下列命题：①函数f（x）的图象关于y轴对称；②函数f（x）的图象关于x轴对称；③函数f（x）的最小值是0；④函数f（x）没有最大值；⑤函数f（x）在（-∞，0）上是减函数，在（0，+∞）上是增函数．其中正确命题的序号是
 
．
下面给出的命题中：
①已知f（n）=12+22+32+…+（2n）2，则f（k+1）与f（k）的关系是f（k+1）=f（k）+（2k+1）2+（2k+2）2．
②已知ξ服从正态分布N（0，σ2），且P（-2≤ξ≤0）=0.4，则P（ξ＞2）=0.2，
③将函数y=cos2x的图象向右平移
π
3
个单位，得到函数y=sin（2x-
π
6
）的图象．
其中是真命题的有
 
．（填序号）
在40根纤维中，有12根的长度超过30mm，从中任取一根，取到长度超过30mm的纤维的概率是
 
．
有6本不同的书，分成四份，每份至少一本，则不同的方法有（　　）
A、110B、45
C、65D、165

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网