题目内容
9.在△ABC中,内角A,B,C所对的边分别为a,b,c,c=2,A≠B.(I)求$\frac{asinA-bsinB}{sin(A-B)}$的值;
(2)若△ABC的面积为1,且tanC=2,求a+b的值.
分析 (1)展开两角差的正弦,利用正弦定理和余弦定理化角为边得答案;
(2)由tanC=2求得$sinC=\frac{2\sqrt{5}}{5},cosC=\frac{\sqrt{5}}{5}$,利用面积及面积公式求得ab的值,再由余弦定理得答案.
解答 解:(1)∵c=2,
∴$\frac{asinA-bsinB}{sin(A-B)}$=$\frac{asinA-bsinB}{sinAcosB-cosAsinB}=\frac{{a}^{2}-{b}^{2}}{acosB-bcosA}$
=$\frac{{a}^{2}-{b}^{2}}{a•\frac{{a}^{2}+{c}^{2}-{b}^{2}}{2ac}-b•\frac{{b}^{2}+{c}^{2}-{a}^{2}}{2bc}}$=$\frac{c({a}^{2}-{b}^{2})}{{a}^{2}-{b}^{2}}=2$;
(2)∵tanC=$\frac{sinC}{cosC}=2$,且sin2C+cos2C=1,
∴$sinC=\frac{2\sqrt{5}}{5},cosC=\frac{\sqrt{5}}{5}$,
∵${S}_{△ABC}=\frac{1}{2}absinC=\frac{1}{2}ab×\frac{2\sqrt{5}}{5}$,∴ab=$\sqrt{5}$,
由余弦定理有cosC=$\frac{\sqrt{5}}{5}=\frac{{a}^{2}+{b}^{2}-{c}^{2}}{2ab}=\frac{{a}^{2}+{b}^{2}-4}{2ab}$,
∴a2+b2=6.
∴$(a+b)^{2}={a}^{2}+{b}^{2}+2ab=6+2\sqrt{5}$,
∴a+b=$\sqrt{5}+1$.
点评 本题考查正弦定理和余弦定理的应用,考查了三角形的解法,是中档题.

| A. | (∁RA)∩B=∅ | B. | (∁RA)∩B=∁RA | C. | (∁RA)∩B=[1,2] | D. | (∁RA)∪B=R |
| A. | 3(3n-2n) | B. | 3n+2n | C. | 3n | D. | 3•2n-1 |
| A. | 2 | B. | 3 | C. | 9 | D. | 11 |
| A. | y=|sinx| | B. | y=tan|x| | C. | y=cosx | D. | y=-cosx |
| A. | B⊆A | B. | A∪B=A | C. | A∩B=B | D. | A∩B={3} |
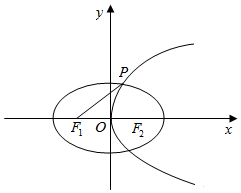 已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的左右焦点分别为F1,F2,抛物线y2=4x与椭圆C有相同的焦点,点P为抛物线与椭圆C在第一象限的交点,且|PF1|=$\frac{7}{3}$.
已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的左右焦点分别为F1,F2,抛物线y2=4x与椭圆C有相同的焦点,点P为抛物线与椭圆C在第一象限的交点,且|PF1|=$\frac{7}{3}$.