题目内容
（1）若PQ是圆x2+y2=9的弦，PQ的中点是（1，2），求弦PQ的长度；
（2）已知圆心为C的圆经过点A（1，1）和B（2，-2），且圆心C在直线l：x-y+1=0上，求圆心为C的圆的标准方程．
（2）已知圆心为C的圆经过点A（1，1）和B（2，-2），且圆心C在直线l：x-y+1=0上，求圆心为C的圆的标准方程．
考点：直线与圆的位置关系,圆的标准方程
专题：计算题,直线与圆
分析：（1）求出弦心距为
，利用勾股定理，计算弦PQ的长度；
（2）根据题意设出圆的标准方程，代入点的坐标，和圆心位置，解方程组即可．
| 5 |
（2）根据题意设出圆的标准方程，代入点的坐标，和圆心位置，解方程组即可．
解答：
解：（1）圆心坐标为（0，0），r=3，弦心距为
，∴|PQ|=2
=4..…（7分）
（2）∵kAB=-3，AB中点（
，-
），∴AB中垂线：x-3y-3=0…．（9分）
由
得圆心坐标C（-3，-2），半径|CA|=5…．（13分）
得圆的标准方程：（x+3）2+（y+2）2=25…..（14分）
| 5 |
| 9-5 |
（2）∵kAB=-3，AB中点（
| 3 |
| 2 |
| 1 |
| 2 |
由
|
得圆的标准方程：（x+3）2+（y+2）2=25…..（14分）
点评：本题主要考查待定系数法求圆的标准．会解方程组是本题的关键．属于基础题．
练习册系列答案
相关题目
设x、y满足
，则（x-1）2+（y-1）2的最小值是（ ）
|
A、
| ||||
B、
| ||||
| C、1 | ||||
| D、2 |
设
表示复数z的共轭复数，则与“复数z为实数”不等价的说法是（ ）
. |
| z |
A、z=
| ||
| B、z2≥0 | ||
C、z+
| ||
| D、lmz=0（lmz表示复数z的虚部） |
设函数f（x）=
，若f（x0）=1，则x0等于（ ）
|
| A、2 | B、-1 | C、1 | D、2或-1 |
将函数y=sin2x的图象向左平移
个单位，再向上平移1个单位，所得图象的函数解析式是（ ）
| π |
| 4 |
| A、y=cos2x | ||
B、y=1+sin(2x+
| ||
| C、y=2cos2x | ||
| D、y=2sin2x |
△ABC的内角A，B，C所对的边a，b，c满足（a+b）2-c2=4，且C=60°，则ab的值为（ ）
A、
| ||
B、8-4
| ||
| C、1 | ||
D、
|
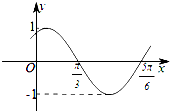已知函数f（x）=sinωx+φ）（ω＞0，0＜φ≤