题目内容
已知数列{an}为等差数列,首项a1=1,公差d≠0.若ab1,ab2,ab3,…,abn,…成等比数列,且b1=1,b2=2,b3=5.
(1)求数列{bn}的通项公式bn;
(2)设cn=log3(2bn-1),求和Tn=c1c2-c2c3+c3c4-c4c5+…+c2n-1c2n-c2nc2n+1.
(1)求数列{bn}的通项公式bn;
(2)设cn=log3(2bn-1),求和Tn=c1c2-c2c3+c3c4-c4c5+…+c2n-1c2n-c2nc2n+1.
考点:数列的求和,等差数列的通项公式,等比数列的性质
专题:等差数列与等比数列
分析:(1)由已知得(1+d)2=1×(1+4d),从而d=2,q=3,由此能求出bn=
.
(2)由cn=log3(2bn-1)=n-1,Tn=c2(c1-c3)+c4(c3-c5)+c6(c5-c7)+…+c2n(c2n-1-c2n+1)=-2(c2+c4+…+c2n),能求出Tn.
| 3n-1+1 |
| 2 |
(2)由cn=log3(2bn-1)=n-1,Tn=c2(c1-c3)+c4(c3-c5)+c6(c5-c7)+…+c2n(c2n-1-c2n+1)=-2(c2+c4+…+c2n),能求出Tn.
解答:
解:(1)∵数列{an}为等差数列,首项a1=1,公差d≠0.
ab1,ab2,ab3,…,abn,…成等比数列,且b1=1,b2=2,b3=5.
∴a22=a1•a5,∴(1+d)2=1×(1+4d),
1+2d+d2=1+4d,
解得d=2或d=0(舍),
ab1=a1=1,ab2=3.∴q=3…(3分)
abn=1+(bn-1)×2=2bn-1=1×3n-1,
∴bn=
…(6分)
(2)cn=log3(2bn-1)=n-1…(7分),
Tn=c2(c1-c3)+c4(c3-c5)+c6(c5-c7)+…+c2n(c2n-1-c2n+1)
=-2(c2+c4+…+c2n)
=-2[1+3+5+…+(2n-1)]
=-2n2…(12分)
ab1,ab2,ab3,…,abn,…成等比数列,且b1=1,b2=2,b3=5.
∴a22=a1•a5,∴(1+d)2=1×(1+4d),
1+2d+d2=1+4d,
解得d=2或d=0(舍),
ab1=a1=1,ab2=3.∴q=3…(3分)
abn=1+(bn-1)×2=2bn-1=1×3n-1,
∴bn=
| 3n-1+1 |
| 2 |
(2)cn=log3(2bn-1)=n-1…(7分),
Tn=c2(c1-c3)+c4(c3-c5)+c6(c5-c7)+…+c2n(c2n-1-c2n+1)
=-2(c2+c4+…+c2n)
=-2[1+3+5+…+(2n-1)]
=-2n2…(12分)
点评:本题考查数列的通项公式和前n项和公式的求法,是中档题,解题时要认真审题,注意等差数列和等比数列的性质的合理运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
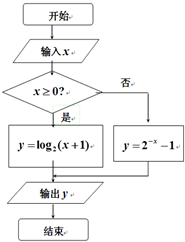
如图所示的程序框图的输出值y∈(1,2],则输入值x的范围是( )

| A、(-∞,3] |
| B、[-1,log23) |
| C、[-log23,-1)∪(1,3] |
| D、[-log23,0)∪(1,3] |
实数x、y满足x2+2xy+y2+4x2y2=4,则x-y的最大值为( )
A、
| ||
B、
| ||
C、
| ||
D、2
|
已知函数f(x)=
,若g(x)=ax-|f(x)|的图象与x轴有3个不同的交点,则实数a的取值范围是( )
|
A、[
| ||||
B、(0,
| ||||
C、(0,
| ||||
D、[
|