题目内容
3．已知实数a，b满足a＞b，且ab=2，则$\frac{{a}^{2}+{b}^{2}+1}{a-b}$的最小值是$2\sqrt{5}$．分析 实数a，b满足a＞b，且ab=2，变形为$\frac{{a}^{2}+{b}^{2}+1}{a-b}$=$\frac{（a-b）^{2}+2ab+1}{a-b}$=（a-b）+$\frac{5}{a-b}$，再利用基本不等式的性质即可得出．
解答 解：∵实数a，b满足a＞b，且ab=2，
∴$\frac{{a}^{2}+{b}^{2}+1}{a-b}$=$\frac{（a-b）^{2}+2ab+1}{a-b}$=（a-b）+$\frac{5}{a-b}$≥2$\sqrt{（a-b）•\frac{5}{a-b}}$=2$\sqrt{5}$，当且仅当$b=\frac{\sqrt{13}-\sqrt{5}}{2}$，a=$\frac{\sqrt{13}+\sqrt{5}}{2}$时取等号．
∴$\frac{{a}^{2}+{b}^{2}+1}{a-b}$的最小值是 2$\sqrt{5}$．
故答案为：2$\sqrt{5}$．
点评 本题考查了基本不等式的性质，考查了推理能力与计算能力，属于中档题．
练习册系列答案
阅读快车系列答案
相关题目
13．已知A，B，P是$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$上不同的三点，且A，B连线经过坐标原点，若直线PA，PB的斜率乘积${k_{PA}}•{k_{PB}}=-\frac{4}{9}$，则的离心率（ ）
| A． | $\frac{{\sqrt{5}}}{2}$ | B． | $\frac{{\sqrt{5}}}{3}$ | C． | $\sqrt{2}$ | D． | $\frac{{\sqrt{15}}}{3}$ |
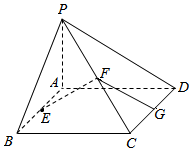如图，已知矩形ABCD所在平面外一点P，PA⊥平面ABCD，E、F、G分别是AB、PC、CD的中点，|PA|=|AB|=|AD|=1，
11．已知集合A={0，l，3}，B={x|x2-3x=0}，则A∩B=（ ）
| A． | {0} | B． | {0，1} | C． | {0，3} | D． | {0，1，3} |
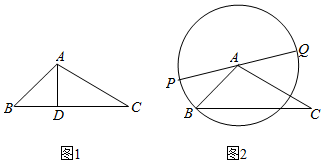在△ABC中．
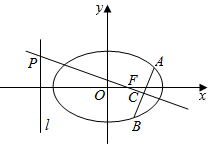如图，在平面直角坐标系xOy中，己知椭圆$\frac{x^2}{2}+{y^2}$=1的右焦点F，直线x=-2，过F的直线与椭圆交于A、B两点（AB与x轴不垂直），线段的垂直平分线分别交直线L和AB于点P、C．若PC=2AB，求直线AB的方程．
15．某班有男、女优秀少先队员各2名，现需选出2名优秀少先队员到社区做公益宣传活动，则选出的两名队员性别相同的概率为（ ）
| A． | $\frac{1}{4}$ | B． | $\frac{1}{3}$ | C． | $\frac{1}{2}$ | D． | $\frac{2}{3}$ |