题目内容
15.在直角坐标系xOy中,已知圆C:$\left\{{\begin{array}{l}{x=2cosθ}\\{y=2sinθ}\end{array}}\right.$(θ为参数),点P在直线l:x+y-4=0上,以坐标原点为极点,x轴的正半轴为极轴,建立极坐标系.( I)求圆C和直线l的极坐标方程;
( II)射线OP交圆C于R,点Q在射线OP上,且满足|OP|2=|OR|•|OQ|,求Q点轨迹的极坐标方程.
分析 (Ⅰ)圆C:$\left\{{\begin{array}{l}{x=2cosθ}\\{y=2sinθ}\end{array}}\right.$(θ为参数),可得直角坐标方程:x2+y2=4,利用互化公式可得圆C的极坐标方程.点P在直线l:x+y-4=0上,利用互化公式可得直线l的极坐标方程.
(Ⅱ)设P,Q,R的极坐标分别为(ρ1,θ),(ρ,θ),(ρ2,θ),由${ρ_1}=\frac{4}{sinθ+cosθ},{ρ_2}=2$,又|OP|2=|OR|•|OQ|,即可得出.
解答 解:(Ⅰ)圆C:$\left\{{\begin{array}{l}{x=2cosθ}\\{y=2sinθ}\end{array}}\right.$(θ为参数),可得直角坐标方程:x2+y2=4,∴圆C的极坐标方程ρ=2.
点P在直线l:x+y-4=0上,直线l的极坐标方程ρ=$\frac{4}{sinθ+cosθ}$.
(Ⅱ)设P,Q,R的极坐标分别为(ρ1,θ),(ρ,θ),(ρ2,θ),
因为${ρ_1}=\frac{4}{sinθ+cosθ},{ρ_2}=2$,
又因为|OP|2=|OR|•|OQ|,即${ρ_1}^2=ρ•{ρ_2}$,∴$ρ=\frac{{{ρ_1}^2}}{ρ_2}=\frac{16}{{{{(sinθ+cosθ)}^2}}}×\frac{1}{2}$,
∴ρ=$\frac{8}{1+sin2θ}$.
点评 本题考查了参数方程、极坐标方程化为直角坐标方程及其应用,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
5.若实数x,y满足不等式组$\left\{\begin{array}{l}{y-x≥0}\\{x+y-7≤0}\\{x≥0}\end{array}\right.$,则z=2x+y的最大值是( )
| A. | $\frac{7}{2}$ | B. | $\frac{21}{2}$ | C. | 14 | D. | 21 |
10.过抛物线y2=4x的焦点F的直线交抛物线于A,B两点,且|AF|=2|BF|,则直线AB的斜率为( )
| A. | $2\sqrt{2}$ | B. | $2\sqrt{3}$ | C. | $2\sqrt{2}$或$-2\sqrt{2}$ | D. | $2\sqrt{3}或-2\sqrt{3}$ |
7.过抛物线y2=4x的焦点F且斜率为$2\sqrt{2}$的直线交抛物线于A,B两点(xA>xB),则$\frac{{|{AF}|}}{{|{BF}|}}$=( )
| A. | $\frac{3}{2}$ | B. | $\frac{3}{4}$ | C. | 3 | D. | 2 |
4.已知集合A={x|x2-2x-3<0},集合B={x|2x-1≥1},则A∩B=( )
| A. | [-1,3) | B. | [0,3) | C. | [1,3) | D. | (1,3) |
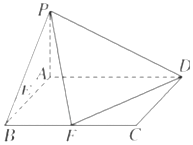 已知在四棱锥P-ABCD中,底面ABCD是矩形,且AD=2,AB=1,PA⊥平面ABCD,E,F分别是线段AB,BC的中点.
已知在四棱锥P-ABCD中,底面ABCD是矩形,且AD=2,AB=1,PA⊥平面ABCD,E,F分别是线段AB,BC的中点.